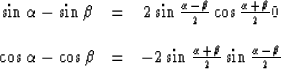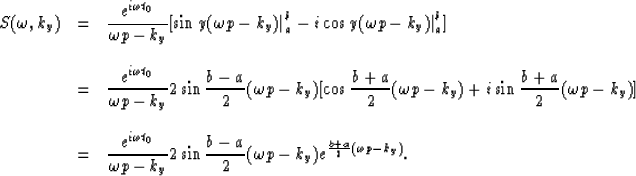Next: About this document ...
Up: Popovici : DMO basics
Previous: MZO by Fourier transform
- Claerbout, J. C., 1985, Imaging the Earth's Interior:
Blackwell Scientific Publications.
- Hale, I. D., 1983, Dip-moveout by Fourier
transform: Ph.D. Thesis, Stanford University.
- Hale, I. D., 1988, Dip-moveout processing:
Course notes from SEG continuing education course, SEG.
- Levin, F. K., 1971,
Apparent velocity from dipping interface reflections:
Geophysics, 36, 510-516.
- Popovici, A. M., and Biondi, B., 1989,
Kinematics of prestack partial migration in a variable velocity medium:
SEP - 61, 133-147.
- Yilmaz, O., and Claerbout, J. F., 1980,
Prestack partial migration:
Geophysics, 45, 1753-1779.
- Zhang, L., 1988,
A new Jacobian for dip-moveout:
SEP - 59, 201-208.
APPENDIX A
The Fourier transform of a finite segment
differs only in the amplitude term from the Fourier transform
of an infinitely long segment. This is to be expected since
we actually multiply the infinite segment by a boxcar filter which
in Fourier domain means convolution with a sync function.
A two dimensional function representing a segment of constant amplitude
in (t,y) space can be described by
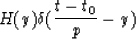
where
![\begin{displaymath}
\left \{ \begin{array}
{ll}
H(y)=1; & y \in [a,b]
\\ \\ H(y)=0; & y \in (-\infty,a) \cup (b,\infty)\end{array} \right.\end{displaymath}](img31.gif)
where t and y are the coordinates,
t0 is the intersection point on the t axis and
the value p is the tangent of the slope.
The function 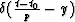 has unitary amplitude
when the argument is zero or t=t0+py.
The 2-D Fourier transform is
has unitary amplitude
when the argument is zero or t=t0+py.
The 2-D Fourier transform is
![\begin{displaymath}
\begin{array}
{lcl}
S(\omega,k_y) & = & \displaystyle{
\int ...
...omega p-k_y)}+i \int_a^b {\sin y(\omega p-k_y)}
] }\end{array}\end{displaymath}](img72.gif)
and using the well known trigonometric transformations
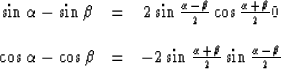
we obtain
| 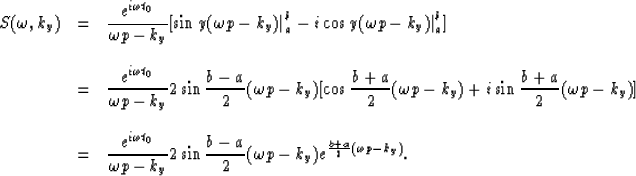 |
(29) |





Next: About this document ...
Up: Popovici : DMO basics
Previous: MZO by Fourier transform
Stanford Exploration Project
11/17/1997
![]()
![\begin{displaymath}
\left \{ \begin{array}
{ll}
H(y)=1; & y \in [a,b]
\\ \\ H(y)=0; & y \in (-\infty,a) \cup (b,\infty)\end{array} \right.\end{displaymath}](img31.gif)
![\begin{displaymath}
\begin{array}
{lcl}
S(\omega,k_y) & = & \displaystyle{
\int ...
...omega p-k_y)}+i \int_a^b {\sin y(\omega p-k_y)}
] }\end{array}\end{displaymath}](img72.gif)