




Next: Hale's DMO
Up: DMO BY FOURIER TRANSFORM
Previous: DMO BY FOURIER TRANSFORM
In order to understand how DMO by Fourier transform works we
have to examine some properties of the 2-D Fourier transform.
In particular the fact that all events with a particular
slope in the time-space domain are mapped to a single
radial line (a line passing through the origin)
in the frequency-wavenumber domain.
A two-dimensional function representing a segment of constant amplitude
in a zero-offset section can be described by
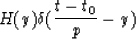
where
![\begin{displaymath}
\left \{ \begin{array}
{ll}
H(y)=1; & y \in [a,b]
\\ \\ H(y)=0; & y \in (-\infty,a) \cup (b,\infty)\end{array} \right.\end{displaymath}](img31.gif)
where t and y are the zero-offset coordinates,
t0 is the intersection point on the time axis and
the value p is the tangent of the slope
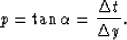
In the corresponding depth model p becomes
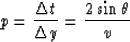
as seen in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The angle
.
The angle 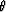 represents
the slope of the reflector in the depth model and
v is the velocity of the medium.
The function
represents
the slope of the reflector in the depth model and
v is the velocity of the medium.
The function 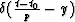 has unitary amplitude
when the argument is zero or
has unitary amplitude
when the argument is zero or 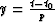 .
dipkxomega
.
dipkxomega
Figure 10 Dipping bed geometry in a constant-offset section and the
corresponding constant velocity depth model. In a zero-offset
section the slope of the reflection is
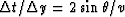 ,where
,where 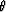 is the dipping angle in the depth model
and v is the velocity.
is the dipping angle in the depth model
and v is the velocity.
 FFT2Ddips
FFT2Ddips
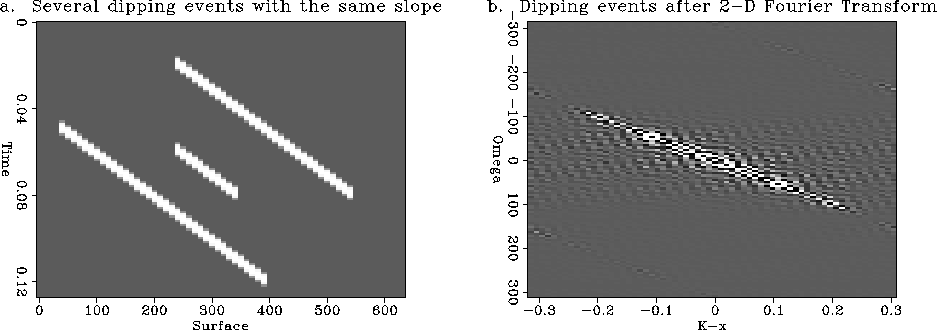
Figure 11 The effect of 2-D Fourier transform on events with same dip.
a. Several reflectors with the same dip in space-time coordinates.
b. The 2-D Fourier transform of the same section. Note that all the
events are mapped on a radial line.

I include in the Appendix a formal derivation for
the analytic solution of a 2-D Fourier transform of a constant
length segment. The 2-D Fourier transform of
an infinite segment is
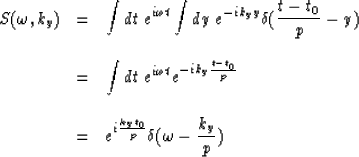
which in the 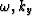 space represents a line
with slope
space represents a line
with slope
|  |
(9) |
In Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .a several dipping segments with the
same slope are all mapped after the Fourier transformation
to a radial line
in Figure
.a several dipping segments with the
same slope are all mapped after the Fourier transformation
to a radial line
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .b in
.b in  space.
space.





Next: Hale's DMO
Up: DMO BY FOURIER TRANSFORM
Previous: DMO BY FOURIER TRANSFORM
Stanford Exploration Project
11/17/1997
![]()
![\begin{displaymath}
\left \{ \begin{array}
{ll}
H(y)=1; & y \in [a,b]
\\ \\ H(y)=0; & y \in (-\infty,a) \cup (b,\infty)\end{array} \right.\end{displaymath}](img31.gif)
![]()
![]()
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The angle
.
The angle 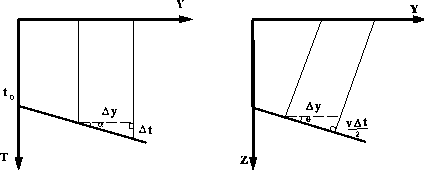
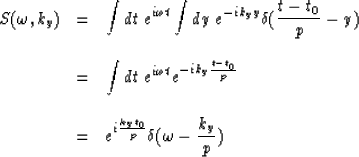
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .a several dipping segments with the
same slope are all mapped after the Fourier transformation
to a radial line
in Figure
.a several dipping segments with the
same slope are all mapped after the Fourier transformation
to a radial line
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .b in
.b in ![]() space.
space.