Wavelets of different orders

Daubechies' 4-point set is only one of a series of compact wavelets. The user chooses an even number of mother coefficients c_k, and the stated conditions of orthogonality and approximation define the wavelet transformation. The case of two coefficients leads to the Haar transform. The recursion matrix is  

$$\left[\matrix{ c_0 & c_1 & & & & & \cr c_0 & -c_1 & & & & ... ...cr & & & & c_0 & c_1 & \cr & & & & c_0 & -c_1 & \cr }\right]$$ (12)

The orthogonality condition requires that

 

c₀² + c₁² = 2

The remaining degree of freedom is used to reach a vanishing momentum of the zeroth order, as follows:

 

c₀ - c₁ = 0

The resulting coefficients c₀ = c₁ = 1 define the Haar transform. Note how the vectors (1,1) and (1,-1) of the matrix (12) realize a simple lowpass and highpass filter. Daubechies wavelets comprise the Haar wavelet as their 2-point member. The Haar transform is much older than the Daubechies wavelets and therefore has its own name.

In general, the orthogonality condition for a Daubechies wavelet transform of order N accounts for N/2 relations of the form  

$$\sum_{k} c_{k} c_{k - 2 m} = 2 \delta_{0 m} ,$$ (15)

where m = 0,1,..,N/2 - 1. The remaining N/2 degrees of freedom are used for achieving a maximum order of polynomial approximation p = N/2 - 1, as follows:  

$$\sum_{k} (-1)^{k} k^{m} c_{k} = 0 ,$$ (16)

for m = 0,1,...,p.

 

copspec
Figure 3 A table of various wavelets. The lines show the the 4, 12, 20 point wavelet filters and their spectrum (1st through 3rd line). The spectrum slope is increased by placing more zeroes at zero frequency. The figures are created by placing impulses in the first octave space in the wavelet domain. The inverse wavelet transform and its Fourier spectrum are displayed. The bottom line depicts a wavelet corresponding to a second octave event. The spectrum is illustrated in the Figure 4.

 

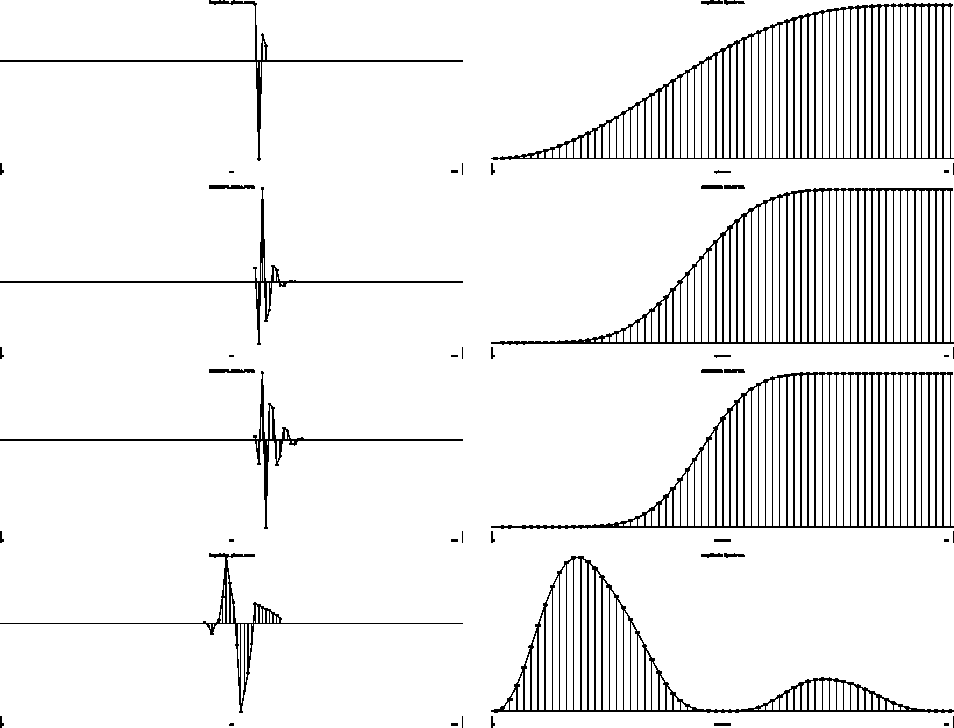
spec Figure 4 Amplitude spectrum of a higher scale wavelet. An impulse in the second octave is convolved by the wavelet operating on the double sample rate. In the next and final recursion, this output is convolved by a set of lowpass coefficients. Concatenation of the convolutions is equivalent to multiplication of the corresponding frequency filter. The first and second lines display the filter for the different recursion steps. The bottom line is the product of both spectra.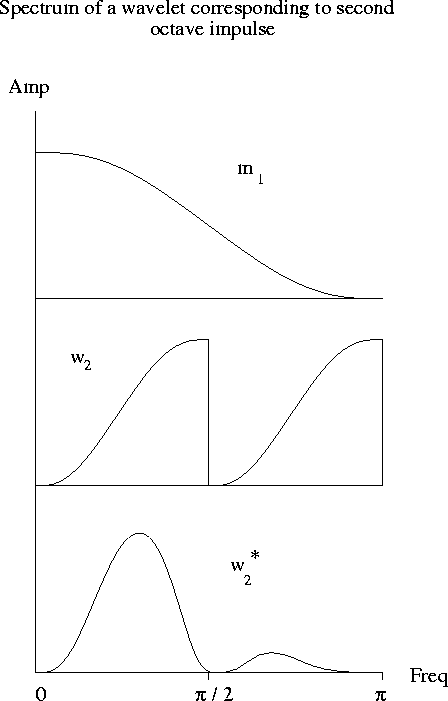

Solving this system of equations and choosing the minimum phase solution yields the N coefficients c_k.