The butterfly

The actual DWT is a recursion of the matrix multiplication described in the preceding section. The original vector B has the length N, which must be a power of 2. Consequently, the first recursion filter C has the dimension $N \times N$. The even N/2 coefficients of the output vector represent the local highpass details w_t. The odd coefficients represent the local lowpass averages m_t. The highpass coefficients are stored in the final result vector. The N/2 odd coefficients m_t, which are the local lowpass averages, enter the next recursion.

In the next recursion step, the matrix C has the dimensions ${N \over 2} \times {N \over 2}$. It operates entirely on the lowpass averages of the previous step. Again, its detail coefficients are stored in the output vector; its averages enter the next recursion step. Consequently, the details w_t and the averages m_t are also called wavelet and mother coefficients, respectively.

When only two coefficients remain in the recursion, the recursion ends. These final two coefficients are averages of previous averages. They complete as top coefficients the final wavelet coefficient vector w_t. Such a series of matrix multiplication and sorting is often referred to as a pyramidal or butterfly structure.

In the following diagram, the subscript of a subvector denotes the recursion of which it is a result. The subscript of each coefficient numbers pairs within the output of a particular recursion.  

$$\left[\matrix{ B_0 \cr B_1 \cr B_2 \cr B_3 \cr B_4 \cr B_5... ...matrix{ w_0 \cr w_1 \cr w_2 \cr w_3 \cr }\right]_1 \end{array}$$ (3)

The inverse DWT transform is performed by interleaving the top four coefficients of the wavelet domain vector, then multiplying them by the corresponding inverse matrix. Recursively applying the inverse operation of the forward matrix multiplication and separation yields the original input vector. The program dwtact.rt implements the recursion.

#
#%
subroutine dwtact(conj, dir, dat,n1,n2,n3, c,nop)
integer           conj, dir,     n1,n2,n3,   nop, n, i1,i2,i3
real 	                     dat(n1,n2,n3),c(nop)

call cofi(dir,c,nop)

Do i3 = 1,n3
Do i2 = 1,n2
  if(conj == 0){
    n = n1
    while( n >= 4 ){
      call dwt(conj, dat((i2-1)*n1+(i3-1)*n2*n1 + 1,1,1) ,n, c,nop)
      n = n/2
  } }
  else{
    n = 4
    while( n <= n1 ){
      call dwt(conj, dat((i2-1)*n1+(i3-1)*n2*n1 + 1,1,1) ,n, c,nop)
      n = 2*n
  } }
return; end

 

ipret
Figure 1 The Impulse response of the 4-point wavelet transformation. The input is a trace of 32 samples showing an impulse at the 26th location. The second half of the DWT trace is the filter coefficients of the 4-point filter applied to the input. The event at the 28th sample, the 12th sample in the first octave, is two samples long. These two samples are the weighted sums of the 4-point filter (bottom trace) passing the impulse in shifts by two. In each subsequent octave (increasing to the right), we can find an event sampling the impulse. These events are the highpass coefficients of the recursion step operating on the lowpass coefficients of the former octave. The active button allows you to build your own input vector and lets you apply various wavelet transforms.

 

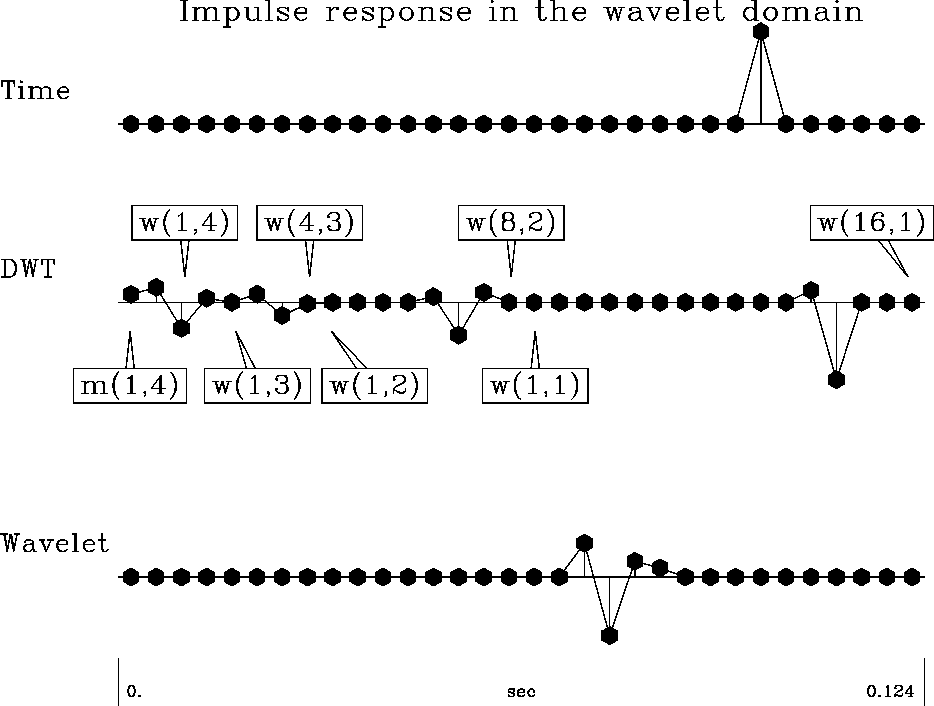loc Figure 2 Localization of a base function in the frequency-time plane. Dots in the frequency-time plane represent the localization corresponding to a certain wavelet coefficient. Each horizontal line refers to coefficients of the same octave. The localization is idealized: the dot represents the first time sample of the filter whose length increases with frequency. The dot's ordinate represents the frequency peak of the filter. For example, an FFT transform would plot as a string of equally spaced dots along the 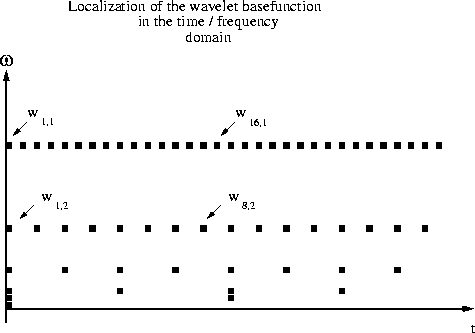$\omega$ axis. (Adapted from Daubechies)