Elastic medium

For the anisotropic elastic case the differential operator 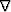$\nabla$ is a 6x3 matrix of partial spatial derivatives and when operating on the displacement field results in the symmetric Lagrange strain tensor.  

$$\nabla^T = {1\over2}({\partial\over{\partial x_l}}+ {\partial\over{\partial x_k}}) \qquad\qquad{\rm with}\qquad k,l=1,2,3$$ (2)

Giving us the following set of first order (in space) equations:

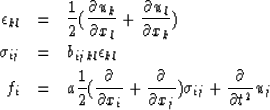$$\begin{eqnarray} \epsilon_{kl} & = & {1\over2}({\partial u_k\over{\partial x_l}}... ...r{\partial x_j}}) \sigma_{ij} +{{\partial}\over{\partial{t^2}}}u_j\end{eqnarray}$$ (3) (4) (5)

where a is the density and b represents the stiffness matrix. In general the stiffness matrix is a sparse matrix, and can be simplified for different degrees of symmetry.