Next: Multiple arrivals
Up: GLOBAL UPDATING SCHEME
Previous: Initialization
From the initial half hexagonal ring on which the attributes of wavefronts
are computed analytically, the process of wavefront propagation follows the
expansion of the ring step by step.
Suppose that the attributes of wavefronts
are known at all the grid points within and on the half hexagonal ring of radius 4
shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . At the grid points on the three sides of the
half-hexagon of radius 5, the attributes of wavefronts
are unknown and to be computed by one step of the updating scheme.
I refer to these grid points as target points.
For each target point, there are six triangular cells attached to it.
Each of these triangular cells has one boundary
across which a local wavefront may propagate towards the target point.
Figure
. At the grid points on the three sides of the
half-hexagon of radius 5, the attributes of wavefronts
are unknown and to be computed by one step of the updating scheme.
I refer to these grid points as target points.
For each target point, there are six triangular cells attached to it.
Each of these triangular cells has one boundary
across which a local wavefront may propagate towards the target point.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows an example in which six boundaries associated
with a target point are labeled from 1 to 6.
Because seismic waves seldom propagate
towards the source point, it is reasonable to assume that
no local wavefront propagates into the half hexagonal ring of radius 5.
With this assumption, local wavefronts that reach the target point must
pass the boundaries 1, 2 or 3 shown in Figure
shows an example in which six boundaries associated
with a target point are labeled from 1 to 6.
Because seismic waves seldom propagate
towards the source point, it is reasonable to assume that
no local wavefront propagates into the half hexagonal ring of radius 5.
With this assumption, local wavefronts that reach the target point must
pass the boundaries 1, 2 or 3 shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Therefore, one step of updating scheme consists of three phases.
In the first phase, the local wavefront passing the boundary 1 is
propagated. The second and third phases propagate the local wavefronts
passing the boundaries 2 and 3, respectively.
Each phase also involves the process of checking the possible diffractions
at the two ends of the corresponding boundary.
.
Therefore, one step of updating scheme consists of three phases.
In the first phase, the local wavefront passing the boundary 1 is
propagated. The second and third phases propagate the local wavefronts
passing the boundaries 2 and 3, respectively.
Each phase also involves the process of checking the possible diffractions
at the two ends of the corresponding boundary.
vpgus
Figure 11 The attributes of wavefronts are known at the grid point
inside and on the half hexagonal ring of radius 4, which are indicated
by small black dots. The large black dot indicates the source point.
Six boundaries associated with a target point are labeled from 1 to 6.

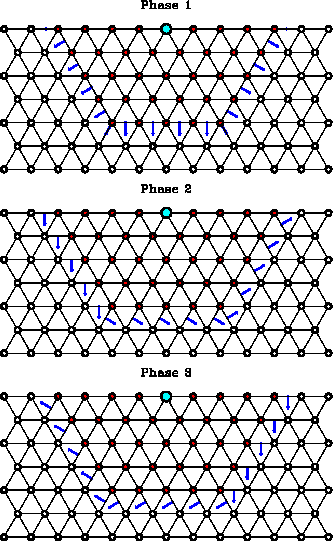
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows how the wavefront propagation in each
of the three phases proceeds globally.
Because the boundary 1 associated with a target point is
always on the half hexagonal ring of radius 4, the attributes of wavefronts
are known at the two ends of the boundary.
Therefore, in the first phase, local wavefronts are propagated towards
the corresponding target points independently.
The situation is different in the second phase.
For each target point, one end of the boundary 2
is at another target point where the attributes of wavefronts may be
unknown. Therefore, local wavefronts are propagated sequentially
and count-clockwise, as shown in Figure
shows how the wavefront propagation in each
of the three phases proceeds globally.
Because the boundary 1 associated with a target point is
always on the half hexagonal ring of radius 4, the attributes of wavefronts
are known at the two ends of the boundary.
Therefore, in the first phase, local wavefronts are propagated towards
the corresponding target points independently.
The situation is different in the second phase.
For each target point, one end of the boundary 2
is at another target point where the attributes of wavefronts may be
unknown. Therefore, local wavefronts are propagated sequentially
and count-clockwise, as shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The propagation of a local wavefront is initiated at a target point
when the attributes of wavefronts are known at the both ends of the
boundary 2 associated with the target point. The propagation terminates
when the attributes of wavefronts are unknown at one end of the boundary 2.
Similarly, in the third phase, local wavefronts are propagated sequentially,
but clockwise.
.
The propagation of a local wavefront is initiated at a target point
when the attributes of wavefronts are known at the both ends of the
boundary 2 associated with the target point. The propagation terminates
when the attributes of wavefronts are unknown at one end of the boundary 2.
Similarly, in the third phase, local wavefronts are propagated sequentially,
but clockwise.
After the three phases of wavefront propagations, the attributes
of wavefronts at all target points are computed. The half hexagonal ring
increases its radius by one grid size for the computation of the next step.
This process is repeated until the expanded half hexagonal ring covers
all the grid points of the given model.
vpupdate
Figure 12 Three phases of the updating scheme in one step of wavefront propagation.
Top: propagating out. Middle: propagating count-clockwise. Bottom:
propagating clockwise. The big black dot shows the source position.
The small black dots inside and on the half hexagonal ring of radius 4 shows
the grid points at which the attributes of the wavefront are known.
The arrows shows that the local wavefronts passing the boundaries attached
by the ends of the arrows are propagated towards the grid points pointed
by the arrows.






Next: Multiple arrivals
Up: GLOBAL UPDATING SCHEME
Previous: Initialization
Stanford Exploration Project
11/17/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . At the grid points on the three sides of the
half-hexagon of radius 5, the attributes of wavefronts
are unknown and to be computed by one step of the updating scheme.
I refer to these grid points as target points.
For each target point, there are six triangular cells attached to it.
Each of these triangular cells has one boundary
across which a local wavefront may propagate towards the target point.
Figure
. At the grid points on the three sides of the
half-hexagon of radius 5, the attributes of wavefronts
are unknown and to be computed by one step of the updating scheme.
I refer to these grid points as target points.
For each target point, there are six triangular cells attached to it.
Each of these triangular cells has one boundary
across which a local wavefront may propagate towards the target point.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows an example in which six boundaries associated
with a target point are labeled from 1 to 6.
Because seismic waves seldom propagate
towards the source point, it is reasonable to assume that
no local wavefront propagates into the half hexagonal ring of radius 5.
With this assumption, local wavefronts that reach the target point must
pass the boundaries 1, 2 or 3 shown in Figure
shows an example in which six boundaries associated
with a target point are labeled from 1 to 6.
Because seismic waves seldom propagate
towards the source point, it is reasonable to assume that
no local wavefront propagates into the half hexagonal ring of radius 5.
With this assumption, local wavefronts that reach the target point must
pass the boundaries 1, 2 or 3 shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Therefore, one step of updating scheme consists of three phases.
In the first phase, the local wavefront passing the boundary 1 is
propagated. The second and third phases propagate the local wavefronts
passing the boundaries 2 and 3, respectively.
Each phase also involves the process of checking the possible diffractions
at the two ends of the corresponding boundary.
.
Therefore, one step of updating scheme consists of three phases.
In the first phase, the local wavefront passing the boundary 1 is
propagated. The second and third phases propagate the local wavefronts
passing the boundaries 2 and 3, respectively.
Each phase also involves the process of checking the possible diffractions
at the two ends of the corresponding boundary.