




Next: LEAST-SQUARES DATUMING
Up: LEAST-SQUARES IMAGING
Previous: Gazdag migration from an
For the finite-difference migration, I tested the 45-degree equation
in 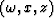 .The velocity model used has a constant gradient from the left upper side
to the right lower side, which is shown in Figure
.The velocity model used has a constant gradient from the left upper side
to the right lower side, which is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (a).
Using this velocity model, a syncline reflector was modeled by the
finite-difference method using the 45-degree equation
and is shown in Figure
(a).
Using this velocity model, a syncline reflector was modeled by the
finite-difference method using the 45-degree equation
and is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (b).
The migration result obtained by the conjugate of the forward modeling
is shown in Figure
(b).
The migration result obtained by the conjugate of the forward modeling
is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (c).
The reflector has clearly imaged except for background artifacts
which seem to be caused by the boundary reflection.
Figure
(c).
The reflector has clearly imaged except for background artifacts
which seem to be caused by the boundary reflection.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (d) shows that we can suppress these artifacts
by using the least-squares imaging method.
Wxz45miginv
(d) shows that we can suppress these artifacts
by using the least-squares imaging method.
Wxz45miginv
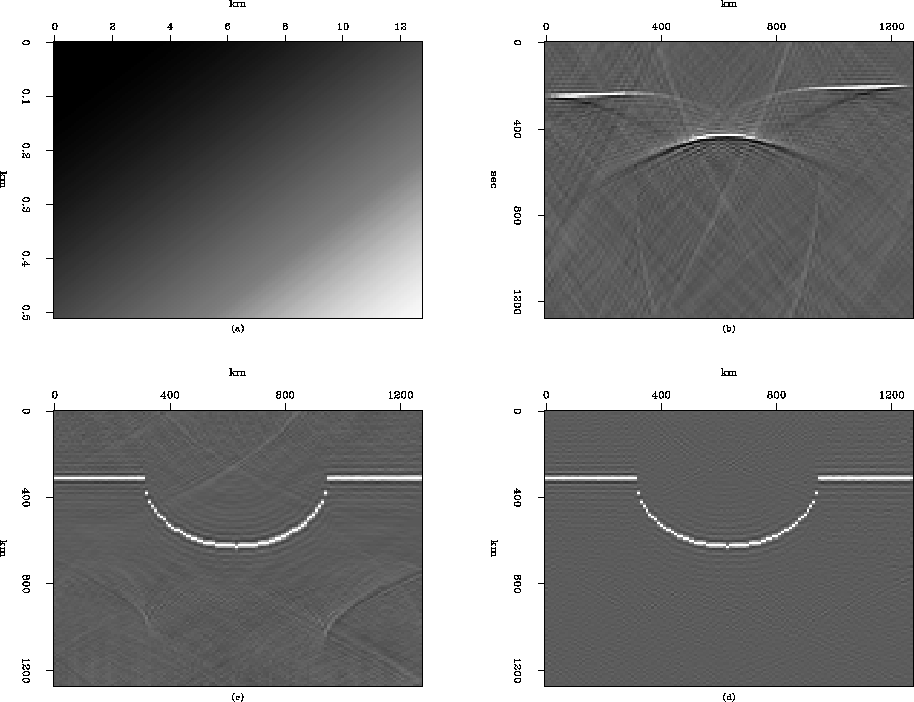
Figure 8 Least-squares finite-difference imaging
in  : (a) The velocity model with a syncline reflector shown in
Figure
: (a) The velocity model with a syncline reflector shown in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (a),
(b) 45-degree finite-difference modeling,
(c) The image obtained by the 45-degree finite-difference
migration for (b),
(d) The image obtained by the least-squares
finite-difference
imaging for (b) (after 10 iterations).
(a),
(b) 45-degree finite-difference modeling,
(c) The image obtained by the 45-degree finite-difference
migration for (b),
(d) The image obtained by the least-squares
finite-difference
imaging for (b) (after 10 iterations).






Next: LEAST-SQUARES DATUMING
Up: LEAST-SQUARES IMAGING
Previous: Gazdag migration from an
Stanford Exploration Project
11/17/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (a),
(b) 45-degree finite-difference modeling,
(c) The image obtained by the 45-degree finite-difference
migration for (b),
(d) The image obtained by the least-squares
finite-difference
imaging for (b) (after 10 iterations).
(a),
(b) 45-degree finite-difference modeling,
(c) The image obtained by the 45-degree finite-difference
migration for (b),
(d) The image obtained by the least-squares
finite-difference
imaging for (b) (after 10 iterations).