




Next: Gazdag migration from an
Up: LEAST-SQUARES IMAGING
Previous: Kirchhoff migration in constant
Gazdag modeling and migration is not a unitary operator
for depth-variable velocity.
As a result, we lose steep dip components of the image
after migration.
The least-squares imaging method can
be used instead to recover the high dip components.
Now the operator in equation (2) becomes the Gazdag modeling operator.
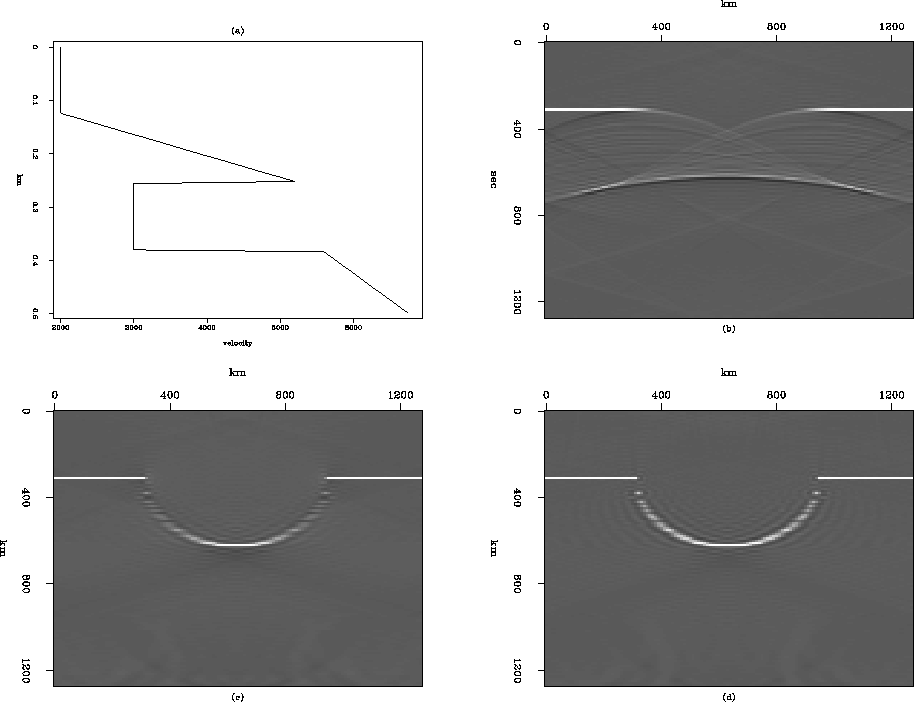
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (a) shows the velocity function used in the experiment,
and the image in the model has the same syncline reflector as
Figure
(a) shows the velocity function used in the experiment,
and the image in the model has the same syncline reflector as
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (a).
The result of the forward Gazdag modeling is shown
in Figure
(a).
The result of the forward Gazdag modeling is shown
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (b).
The image obtained by the migration of this data
is shown in Figure
(b).
The image obtained by the migration of this data
is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (c) and we can see that the steep dip
components is weakly imaged in comparison to the original model.
The image obtained by the least-squares imaging of the same
data, shown in Figure
(c) and we can see that the steep dip
components is weakly imaged in comparison to the original model.
The image obtained by the least-squares imaging of the same
data, shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (d),
shows more steep dip energy.
Gazmiginv
(d),
shows more steep dip energy.
Gazmiginv
Figure 6 Least-squares Gazdag imaging:
(a) The velocity model for the syncline
reflector shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (a),
(b) Gazdag modeling,
(c) The image obtained by the Gazdag migration for (b),
(d) The image obtained by the least-squares Gazdag
imaging for (b) (after 10 iterations).
(a),
(b) Gazdag modeling,
(c) The image obtained by the Gazdag migration for (b),
(d) The image obtained by the least-squares Gazdag
imaging for (b) (after 10 iterations).






Next: Gazdag migration from an
Up: LEAST-SQUARES IMAGING
Previous: Kirchhoff migration in constant
Stanford Exploration Project
11/17/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (a),
(b) Gazdag modeling,
(c) The image obtained by the Gazdag migration for (b),
(d) The image obtained by the least-squares Gazdag
imaging for (b) (after 10 iterations).
(a),
(b) Gazdag modeling,
(c) The image obtained by the Gazdag migration for (b),
(d) The image obtained by the least-squares Gazdag
imaging for (b) (after 10 iterations).