




Next: REFERENCES
Up: Claerbout: Canonical Gazdag routine
Previous: INTRODUCTION
Many situations in physics are expressed by the differential equation
| 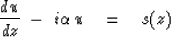 |
(1) |
In the migration application,
u(z) is the up-coming wave,
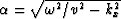 ,s(z) is the ``exploding-reflector'' source,
and
,s(z) is the ``exploding-reflector'' source,
and
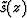 (summed over frequency) is the derived image.
We take the medium to be layered
(v constant in layers)
so that
(summed over frequency) is the derived image.
We take the medium to be layered
(v constant in layers)
so that  is constant in a layer,
and we put the sources at the layer boundaries.
Thus within a layer we have
is constant in a layer,
and we put the sources at the layer boundaries.
Thus within a layer we have 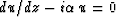 which has the solution
which has the solution
| 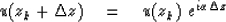 |
(2) |
For convenience, I introduce the ``delay'' operator
in the k-th layer
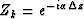 so the delay of upward propagation is expressed by
so the delay of upward propagation is expressed by
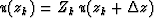 .Besides crossing layers, we must cross layer boundaries
where the (reflection) sources add in
to the upcoming wave.
Thus we have
.Besides crossing layers, we must cross layer boundaries
where the (reflection) sources add in
to the upcoming wave.
Thus we have
| 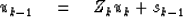 |
(3) |
Recursive use of equation (3) across a medium
of three layers is expressed in matrix form as
| ![\begin{displaymath}
\bold M \, \bold u \quad = \quad
\left[
\begin{array}
{cccc...
... s_1 \\ s_2 \\ s_3
\end{array} \right]
\quad = \quad\bold s\end{displaymath}](img11.gif) |
(4) |
A recursive solution begins at the bottom
with u3=s3 and propagates upward.
The conjugate of the delay operator Z
is the time advance operator 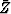 .The conjugate operation to that in equation (4)
is given by
.The conjugate operation to that in equation (4)
is given by
| ![\begin{displaymath}
\bold M' \, \tilde {\bold s} \quad = \quad
\left[
\begin{ar...
..._1 \\ u_2 \\ u_3
\end{array} \right] \
\quad = \quad\bold u\end{displaymath}](img13.gif) |
(5) |
The conjugacy of equation (4) and (5)
seems obvious,
but it is not quite the elementary form we are so familiar with
because the matrix multiplies the output
(instead of the customary matrix multiplying the input).
To prove the conjugacy, notice that
equation (4)
is equivalent to 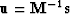 whose
conjugate, by definition,
is
whose
conjugate, by definition,
is 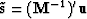 which
is
which
is 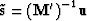 (because of the basic mathematical fact
that the conjugate of an inverse is the inverse of the conjugate)
which gives
(because of the basic mathematical fact
that the conjugate of an inverse is the inverse of the conjugate)
which gives 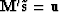 which is equation (5).
which is equation (5).
We observe the wavefield only on the surface z=0,
so the conjugacy of equations (4) and (5)
is academic
because it relates the wavefield at all depths with
the source at all depths.
Thus we need to truncate  to its first coefficient u0.
That will change the conjugate relation.
Remember that the conjugate to truncation is zero padding.
Thus the conjugate to solving
equation (4)
and then abandoning the (unobservable) waves beneath the surface is
the solution to
to its first coefficient u0.
That will change the conjugate relation.
Remember that the conjugate to truncation is zero padding.
Thus the conjugate to solving
equation (4)
and then abandoning the (unobservable) waves beneath the surface is
the solution to
| ![\begin{displaymath}
\bold M' \, \tilde {\bold s} \quad = \quad
\left[
\begin{ar...
...begin{array}
{c}
u_0 \\ 0 \\ 0 \\ 0
\end{array} \right] \\ end{displaymath}](img19.gif) |
(6) |
which amounts to a recursion
beginning from 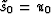 and continuing downward with
and continuing downward with
| 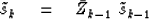 |
(7) |
A final feature of the migration application
is that the image is formed from 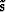 by summing over all frequencies.
The proposed subroutine is
by summing over all frequencies.
The proposed subroutine is
# Phase shift modeling and migration. (Warning: destroys its input!)
#
subroutine gazconj( conj, dt,dx, v,nt,nx, modl, data )
integer conj, nt,nx, iw, ikx, iz,nz
complex iktau, modl(nt,nx), data(nt,nx)
real dt,dx, v(nt), pi, w,w0,dw, kx,kx0,dkx
temporary complex cs(nt)
call conjnull( conj, 0, modl,2*nt*nx, data,2*nt*nx )
pi = 4.*atan(1.); w0 = -pi/dt; dw = 2.*pi/(nt*dt)
nz = nt; kx0 = -pi/dx; dkx= 2.*pi/(nx*dx)
if( conj == 0) call ft2axis( 0, -1., nz, nx, modl)
else { call ft2axis( 0, -1., nt, nx, data)
call ft1axis( 0, 1., nt, nx, data)
}
do ikx = 2, nx { kx = kx0 + (ikx-1) * dkx
do iw = 2, nt { w = w0 + (iw -1) * dw
if( conj== 0) { data(iw,ikx) = modl(nz,ikx)
do iz = nz-1, 1, -1
data(iw,ikx) = data(iw,ikx) * iktau(dt,w,v(iz)*kx,dw) +
modl(iz,ikx)
}
else { cs( 1) = data(iw,ikx)
do iz = 1, nz-1
cs(iz+1) = cs(iz) * conjg( iktau(dt,w,v(iz)*kx,dw) )
do iz = 1, nz
modl(iz,ikx) = modl(iz,ikx) + cs(iz)
}
}}
if( conj == 0) { call ft1axis( 1, 1., nt, nx, data)
call ft2axis( 1, -1., nt, nx, data) }
else { call ft2axis( 1, -1., nz, nx, modl) }
return; end
complex function iktau( dt, w, vkx, nyep)
real dt, w, vkx, nyep # nyep = nyquist * epsilon
iktau = cexp( - dt * csqrt( cmplx( nyep, w) ** 2 + vkx * vkx /4. ) )
return; end





Next: REFERENCES
Up: Claerbout: Canonical Gazdag routine
Previous: INTRODUCTION
Stanford Exploration Project
11/17/1997
![\begin{displaymath}
\bold M \, \bold u \quad = \quad
\left[
\begin{array}
{cccc...
... s_1 \\ s_2 \\ s_3
\end{array} \right]
\quad = \quad\bold s\end{displaymath}](img11.gif)
![]() .The conjugate operation to that in equation (4)
is given by
.The conjugate operation to that in equation (4)
is given by
![\begin{displaymath}
\bold M' \, \tilde {\bold s} \quad = \quad
\left[
\begin{ar...
..._1 \\ u_2 \\ u_3
\end{array} \right] \
\quad = \quad\bold u\end{displaymath}](img13.gif)
![]() to its first coefficient u0.
That will change the conjugate relation.
Remember that the conjugate to truncation is zero padding.
Thus the conjugate to solving
equation (4)
and then abandoning the (unobservable) waves beneath the surface is
the solution to
to its first coefficient u0.
That will change the conjugate relation.
Remember that the conjugate to truncation is zero padding.
Thus the conjugate to solving
equation (4)
and then abandoning the (unobservable) waves beneath the surface is
the solution to
![\begin{displaymath}
\bold M' \, \tilde {\bold s} \quad = \quad
\left[
\begin{ar...
...begin{array}
{c}
u_0 \\ 0 \\ 0 \\ 0
\end{array} \right] \\ end{displaymath}](img19.gif)
![]() by summing over all frequencies.
The proposed subroutine is
by summing over all frequencies.
The proposed subroutine is