




Next: An analogy: the lively
Up: Muir: Inertia tensor
Previous: Further metamorphosis of the
So long as R is isotropic, then it will commute with 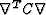 and there will be a Christoffel-like representation. If R
is not isotropic then the following trick will get around the problem.
First, premultiply the equation by R-1/2, which I define as the
symmetric (but possibly complex) matrix whose eigenvalues have a positive
real part, and are the inverse of the square-root of the eigenvalues of the
matrix R, which, for physical reasons (causality, no energy gain), are
also constrained. So equation (4), dropping the
and there will be a Christoffel-like representation. If R
is not isotropic then the following trick will get around the problem.
First, premultiply the equation by R-1/2, which I define as the
symmetric (but possibly complex) matrix whose eigenvalues have a positive
real part, and are the inverse of the square-root of the eigenvalues of the
matrix R, which, for physical reasons (causality, no energy gain), are
also constrained. So equation (4), dropping the 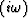 notation, can
be written as,
notation, can
be written as,
| 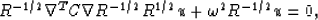 |
(5) |
and this can be further simplified by replacing the displacement field
variable, u, by an energy-like field variable, w, defined equal
to R1/2u. Our final form is now,
| 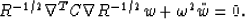 |
(6) |
This new field variable is quite similar to the energy flux variable
introduced by Clint Frasier and reported in Aki & Richards (1980),
although our motivations are somewhat different.





Next: An analogy: the lively
Up: Muir: Inertia tensor
Previous: Further metamorphosis of the
Stanford Exploration Project
11/17/1997