




Next: About this document ...
Up: Bevc: Wave-equation datuming
Previous: DISCUSSION AND CONCLUSION
- Berryhill, J. R., 1979, Wave equation datuming: Geophysics, 44, no. 8, 1329-1344.
-
- Berryhill, J. R., 1984, Wave equation datuming before stack (short note): Geophysics, 49, no. 11, 2064-2067.
-
- Berryhill, J. A., 1986, Submarine canyons - velocity replacement by wave equation datuming before stack: Geophysics, 51, no. 8, 1572-1579.
-
- Bevc, D., 1992, Wave-equation extrapolation of land data with irregular acquisition topography: SEP-73, 301-304.
-
- Claerbout, J. F., 1992, Anti aliasing: SEP-73, 371-390.
-
- Fowler, P., 1988, Seismic velocity estimation using prestack time migration: SEP-58.
-
- Ji, J., and Claerbout, J. F., 1992, Phase shift datuming and migration from an irregular surface: SEP-75, 157-170.
-
- McMechan, G. A., and Chen, H. W., 1990, Implicit static corrections in prestack migration of common-source data: Geophysics, 55, no. 6, 757-760.
-
- Popovici, A. M., 1992, Wave-equation datuming in variable velocity media: SEP-75, 191-214.
-
- Reshef, M., 1991, Depth migration from irregular surfaces with depth extrapolation methods (short note): Geophysics, 56, no. 1, 119-122.
-
- Schneider, W. A., 1978, Integral formulation for migration in two-dimensions and three-dimensions: Geophysics, 43, no. 1, 49-76.
-
- Shtivelman, V., and Canning, A., 1988, Datum correction by wave equation extrapolation: Geophysics, 53, no. 10, 1311-1322.
-
- Wiggins, J. W., 1984, Kirchhoff integral extrapolation and migration of nonplanar data: Geophysics, 49, no. 8, 1239-1248.
-
- Yilmaz, O., and Lucas, D., 1986, Prestack layer replacement: Geophysics, 51, no. 7, 1355-1369.
-
- Zhang, L., and Claerbout, J. F., 1992, Wave-equation resampling of unevenly spaced traces: SEP-75, 243-250.
-
APPENDIX A
In this Appendix I review the derivation of the expression for upward
continuation of a scalar wavefield given by
Berryhill 1979.
The Kirchhoff integral equation Schneider (1978) may be written
for an up-going scalar wavefield U(x,y,z,t) as
| ![\begin{displaymath}
U(x,y,z,t)=\frac{1}{2\pi}\int dA \frac{\cos\theta}{r^2}
\lef...
...
\frac{\partial}{\partial t}U(x_0,y_0,z_0,t-\frac{r}{c})\right]\end{displaymath}](img9.gif) |
(3) |
where the wavefield is known for all points (x0,y0,z0) and for all time
on the planar surface A.
By performing the two-dimensional integral
the wavefield can be expressed at any point above the planar surface.
If the wavefield is
only known along a line in the plane and is assumed to be independent of the
coordinate perpendicular to this line, the integration can be carried out
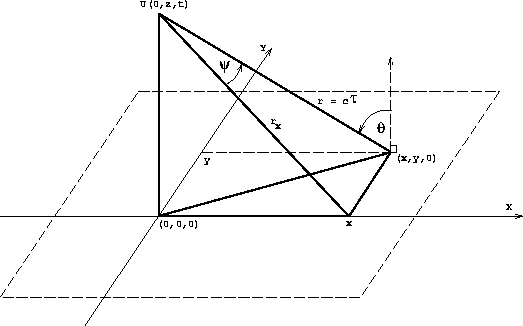
over the perpendicular coordinate. The geometry of this situation is
illustrated in Figure A-A-1 where the
wave field is recorded along the
x direction and is assumed to be constant in the y direction.
Following Berryhill 1979 the integral over dA is performed
for an observation point U(0,z,t) directly above the origin of the
coordinate axes:
| ![\begin{displaymath}
U(0,z,t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}dx \;z \int_{-...
...ac{r}{c}
\frac{\partial}{\partial t}U(x,0,t-\frac{r}{c})\right]\end{displaymath}](img10.gif) |
(4) |
datumfig1
Figure 12 Geometry for the upward continuation of a wavefield.
|
|  |

In order to do the integration in the y direction the following substitutions
can be made according to Figure A-A-1:
Thus the integration in y can be expressed as an integration in  :
:
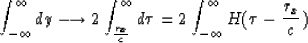
where H is the Heavyside function.
Inserting these substitutions into equation (A-2):
| ![\begin{eqnarray}
U(0,z,t)&=&\frac{1}{\pi}\int_{-\infty}^{\infty}dx \frac{z}{c}
\...
...[U(x,0,t-\tau)+\tau\frac{\partial}{\partial t}U(x,0,t-\tau)\right]\end{eqnarray}](img14.gif) |
|
| (5) |
Equation (A-A-3) is of the form of a convolution in time.
For reference
I write the general form of the convolution integral as:
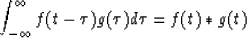
where 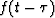 corresponds to
corresponds to 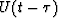 . Defining
. Defining
![\begin{displaymath}
G(\tau)=H(\tau-\frac{r_x}{c})
\left[\frac{1}{\tau^2}\frac{1}{\sqrt{\tau^2-\frac{r_x^2}{c^2}}}\right]\end{displaymath}](img18.gif)
Equation (A-A-3) can
now be written as (looking only at the time part):
![\begin{displaymath}
U(0,z,t) \propto \int_{-\infty}^{\infty}d\tau G(\tau)
\left[U(x,0,t-\tau)+\tau\frac{\partial}{\partial t}U(x,0,t-\tau)\right]\end{displaymath}](img19.gif)
noting that:
![\begin{displaymath}
U(x,0,t) \ast \left[H(t-\frac{r_x}{c})
\frac{1}{t^2\sqrt{t^...
...{r_x}{c})
\frac{c^2\sqrt{t^2-\frac{r_x^2}{c^2}}}{tr_x^2}\right]\end{displaymath}](img20.gif)
and
![\begin{displaymath}
\frac{d}{dt}\left[H(t-\frac{r_x}{c})
\frac{c^2\sqrt{t^2-\fra...
...] =
H(t-\frac{r_x}{c})\frac{1}{t^2\sqrt{t^2-\frac{r_x^2}{c^2}}}\end{displaymath}](img21.gif)
Equation (A-A-3) can now be written as:
| ![\begin{eqnarray}
U(0,z,t)&=&\frac{1}{\pi}\int_{-\infty}^{\infty}dx \frac{z}{c^2}...
...{c^2}}}{tr_x^2} +
\frac{1}{t^2\sqrt{t^2-\frac{r_x^2}{c^2}}}\right]\end{eqnarray}](img22.gif) |
|
| (6) |
summing the terms in brackets and using the definition of the angle 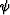 from Figure A-A-1 where
from Figure A-A-1 where
| 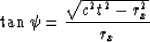 |
(7) |
The integrand in equation (A-A-4) can be written as
| ![\begin{eqnarray}
Q(t-\frac{r_x}{c}) &=& \frac{dU(x,0,t)}{dt} \ast
\left[H(t-\fr...
...,0,t) \ast \left[H(t-\frac{r_x}{c})\frac{d^2\tan\psi}{dt^2}\right]\end{eqnarray}](img25.gif) |
|
| (8) |
Finally the expression for the upward continued wavefield is written as
| 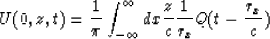 |
(9) |
This is equation (1) of the main text.
For a wavefield transformation from one datum U(x,z=z1 ,t) to
another U(x,z=z2 ,t) the discrete form of equation (A-7) is
a summation.
Each individual trace Uj (t) comprising U(x,z=z2 ,t) is calculated by
performing the sum:
| 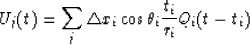 |
(10) |
where Qi(t-ti) is a filtered input trace recorded at location i
and delayed by traveltime ti. This filtering is performed according
to equation (A-A-6).
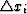 is the input trace interval,
is the input trace interval, 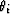 is the angle between
the normal to the surface at z=z2 and the line ri connecting Uj and
Ui. The geometry of the transformation is illustrated in
Figure 1 of the main text.
is the angle between
the normal to the surface at z=z2 and the line ri connecting Uj and
Ui. The geometry of the transformation is illustrated in
Figure 1 of the main text.
The effect of the filtering operation implied by equation (A-A-6) is to
perform a phase-shift of the traces input to the datuming algorithm. This
is illustrated in Figure A-2. The input trace is
convolved with the second derivative of 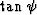 to produce the
output trace which goes into the summation of equation (A-8).
The
to produce the
output trace which goes into the summation of equation (A-8).
The 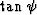 filter is tapered to eliminate undesirable truncation effects.
filter is tapered to eliminate undesirable truncation effects.
For downward continuation, the input traces are crosscorrelated with
the 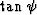 filter after the summation of equation (A-8) has been
performed on the unfiltered traces.
filter after the summation of equation (A-8) has been
performed on the unfiltered traces.
quedemo
Figure 13 The wavelet (upper left) is convolved with the second derivative of 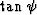 (upper right) to yield the phase shifted trace (bottom). (upper right) to yield the phase shifted trace (bottom).
|
|  |










Next: About this document ...
Up: Bevc: Wave-equation datuming
Previous: DISCUSSION AND CONCLUSION
Stanford Exploration Project
11/17/1997

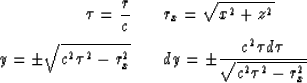
![]()
![\begin{eqnarray}
U(0,z,t)&=&\frac{1}{\pi}\int_{-\infty}^{\infty}dx \frac{z}{c}
\...
...[U(x,0,t-\tau)+\tau\frac{\partial}{\partial t}U(x,0,t-\tau)\right]\end{eqnarray}](img14.gif)
![]()
![\begin{displaymath}
G(\tau)=H(\tau-\frac{r_x}{c})
\left[\frac{1}{\tau^2}\frac{1}{\sqrt{\tau^2-\frac{r_x^2}{c^2}}}\right]\end{displaymath}](img18.gif)
![]()
![\begin{displaymath}
U(x,0,t) \ast \left[H(t-\frac{r_x}{c})
\frac{1}{t^2\sqrt{t^...
...{r_x}{c})
\frac{c^2\sqrt{t^2-\frac{r_x^2}{c^2}}}{tr_x^2}\right]\end{displaymath}](img20.gif)
![\begin{displaymath}
\frac{d}{dt}\left[H(t-\frac{r_x}{c})
\frac{c^2\sqrt{t^2-\fra...
...] =
H(t-\frac{r_x}{c})\frac{1}{t^2\sqrt{t^2-\frac{r_x^2}{c^2}}}\end{displaymath}](img21.gif)
![\begin{eqnarray}
U(0,z,t)&=&\frac{1}{\pi}\int_{-\infty}^{\infty}dx \frac{z}{c^2}...
...{c^2}}}{tr_x^2} +
\frac{1}{t^2\sqrt{t^2-\frac{r_x^2}{c^2}}}\right]\end{eqnarray}](img22.gif)
![\begin{eqnarray}
Q(t-\frac{r_x}{c}) &=& \frac{dU(x,0,t)}{dt} \ast
\left[H(t-\fr...
...,0,t) \ast \left[H(t-\frac{r_x}{c})\frac{d^2\tan\psi}{dt^2}\right]\end{eqnarray}](img25.gif)
![]() to produce the
output trace which goes into the summation of equation (A-8).
The
to produce the
output trace which goes into the summation of equation (A-8).
The ![]() filter is tapered to eliminate undesirable truncation effects.
filter is tapered to eliminate undesirable truncation effects.
![]() filter after the summation of equation (A-8) has been
performed on the unfiltered traces.
filter after the summation of equation (A-8) has been
performed on the unfiltered traces.
