KIRCHHOFF DATUMING

Berryhill 1979 gives the following expression for the upward continuation of a scalar wavefield:  

$$U(0,z,t)=\frac{1}{\pi}\int_{-\infty}^{\infty}dx \frac{z}{c} \frac{1}{r_x} Q(t-\frac{r_x}{c})$$ (1)

where U(0,z,t) is one trace of the upward continued wavefield at datum elevation z and lateral position x=0. The function Q is a time delayed filtered version of the input traces on the original datum. The derivation of this equation is reviewed in the Appendix. Two major assumptions go into the derivation of equation (1):

• The wavefield is two-dimensional and does not vary perpendicular to the seismic line.
• The data are collected on a planar surface.

Despite these assumptions, the algorithm based on this integral produces satisfactory results. The assumptions are locally valid for non-planar datums.

For a wavefield transformation from one datum U(x,z=z₁ ,t) to another U(x,z=z₂ ,t) (Figure 1) the discretized form of equation (1) is a summation. Each individual trace U_j (t) comprising U(x,z=z₂ ,t) is calculated by performing the sum:  

$${U_j (t)= \sum_j \triangle x_i \cos \theta_i {t_i \over r_i} Q_i(t-t_i)}$$ (2)

where Q_i(t-t_i) is a filtered input trace recorded at location i along the lower datum and delayed by traveltime t_i. This filtering operation is described in the Appendix. The effect of the filtering operation is to perform a phase-shift of the traces input to the datuming algorithm. $\triangle x_i$ is the input trace interval, $\theta_i$ is the angle between the normal to the surface at z=z₂ and the line r_i connecting U_j and U_i.

 

datumfig2 Figure 1 Geometry for the continuation of a wavefield between an irregular topography and a planar datum.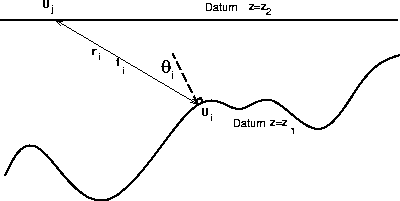

Equations (1) and  (2) are used for upward continuation. For downward continuation the conjugate process is used. The sum is performed first and then the output traces are crosscorrelated with the $\tan\psi$ filter described in the Appendix.

The program for upward and downward continuation is illustrated by the following pseudo-code:

loop over j {
loop over i {
     shift = time shift between input and output trace
     if ( conj != 0 )
          Q = down [convolve] filter
     loop over time {
          if ( conj == 0 )
               Q(time-shift,i) = Q(time-shift,i) + up(time,j)
          else
               up(time,j)         = up(time,j)   + Q(time-shift,i)
                    }
     if ( conj == 0 )
          down = up [crosscorrelate] filter
     }}

The notation in the pseudo-code is consistent with Figure 1. The data on the upper datum z=z₂ corresponds to index j and the data on the lower datum z=z₁ corresponds to index i. For conj!=0 the data are upward continued from down to up and for conj==0 the data are downward continued.

The actual code used to perform the datuming in this paper is complicated by calculation of geometrical parameters which arise due to non-planar datums and by the incorporation of anti-aliasing. Since the datuming algorithm is based on an integral equation solution it is susceptible to operator aliasing. This is taken care of by calculating triangular smoothing functions along the operator trajectory in a manner analogous to Claerbout 1992.