![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)




Next: About this document ...
Up: Table of Contents
SEP-73 -- TABLE OF CONTENTS
Processing
Multi-component source equalization (ps 354K) (src 2708K)
Karrenbach M.
Source equalization is necessary when source
behavior changes with location within a
given survey. Conventional robust methods characterize source differences as
pure amplitude variations, assuming identical source time functions.
I am extending this idea to vector wave fields, with the aim of
preparing the data to be useful in elastic parameter determination (not
just imaging). The method I have employed estimates source-location and
source-component-consistent differences in the data. Those differences are
parameterized as short 1-D filters in time and consequently correct the
data to an average isotropic response. This is a meant to be a step
toward the goal of determining absolute radiation patterns.
Determining the exact radiation pattern is a more difficult task and
requires an estimate of subsurface parameters, while the method shown
here works without one having to know any medium properties.
The source equalization solves a least squares problem in a way that
is consistent in regard to source-location
and source-component without trying to shape the wavelet
as done in surface-consistent deconvolution. The least squares problem
is solved in the time domain using the conjugate gradient method.
Results from a 9-component land data set show that this procedure
equalizes the data mostly by doing differential rotations and slight
modifications of the source time function. The algorithm, although designed
for multi-component data, is directly applicable to conventional single
component data.
Decomposing marine pressure data into a vector wavefield (ps 2152K) (src 6460K)
Filho C. A. C.
Elastic modeling or migration of data recorded in a marine environment
can be formulated as a coupled acoustic-elastic problem with a common
boundary condition at the sea floor. A simpler alternative is to
solve only the elastic wave equation, with vanishing shear moduli within
the water layer. To enable the application of this approach
to real problems, it is necessary to transform the recorded scalar pressure
wavefield into a vector particle-displacement field.
In this paper I describe a method to perform such vectorization
of recorded marine data which is completely independent of the
subsurface geology. Few assumptions are required for the theoretical
justification of the method, the most important being that the depth of
the cable is a smooth function of the receiver position. The wavefield
vectorization is obtained through a simple, inexpensive, linear operation
in the frequency-horizontal wavenumber domain.
Except for a small reduction in the spectral resolution, good results
were obtained when the method was applied to both synthetic
and real data.
Robust wavelet deconvolution (ps 170K) (src 648K)
Mo L.
Conventional wavelet deconvolution ``flattens'' the signal frequency
band and amplifies random noise. We present a method in this note that
``flattens'' the wavelet (signal) frequency band
without amplifying random noise.
It is a modified version of conventional wavelet decon.
The method uses a decimated autocorrelation to compute the inverse wavelet
at a coarser sampling interval.
The order of decimation depends on the signal frequency
range, relative to the full Nyquist frequency.
...
Multiple attenuation using Abelian group theory (ps 500K) (src 9437K)
Mo L.
This paper assumes a flat layered earth model and
offset recording geometry.
We apply velocity transform on the
space-time shot gather into a domain, each of whose attributes forms
an Abelian group. An attribute that is addable irrespective of
ordering forms an Abelian (or commutative) group. Several attributes
form Abelian groups.
We implement two of them at this stage, the
zero-offset two way travel time T, and Dix's parameter
T.Vnmo2.
Addability of attributes dictates that in this domain
sets of multiples - both primary
and multiples - lie at even intervals along parallel straight lines.
The next
most important property of an Abelian group is closure;
in other words, linear
combination of different Abelian group attributes
also forms an Abelian group. We
form linear combination of the T and T.Vnmo2 to steer the
waterbottom multiples and peglegs straight down the T axis.
The periodic character of reverberation events in this domain helps
design predictive multiple attenuation operators.
We apply predictive deconvolution on this domain to attenuate the
waterbottom multiples and peglegs. Then we conjugate velocity transform
the deconned result back to the space-time domain. We test the method
on a Solid elastic model synthetic dataset and on real data. The results
show the efficacy of the method to attenuate waterbottom multiples
and peglegs simultaneously. Theoretically,
recursive application of the procedure
will attenuate all deep earth intrabed multiples. However,
problems remain for this method in velocity transform,
and we point out them in this paper.
The seismic data compression limitations of the singular value decomposition (ps 1369K) (src 1364K)
Abma R.
Reflection seismic data require large volumes of digital storage at a great
cost to the seismic industry.
This cost could be reduced if a compression technique suitable to these
data was found.
Data compression using the singular value decomposition
is examined here in an attempt to reduce this cost.
When any significant compression factor was used,
this compression technique reconstructed the original data poorly
because dipping events and high-frequency detail were lost.
While other seismic
data may be compressed with this method, the compression of
reflection seismic data with the singular-value-decomposition
technique is not practical.
Seismic data processing with Mathematica![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) (ps 850K) (src 1484K)
(ps 850K) (src 1484K)
Abma R.
When treated as vectors or matrices, seismic traces may be
manipulated with Mathematica's large set of mathematical algorithms
and displayed in a variety of presentations. A program for converting
seismic files into Mathematica format and examples of
Mathematica processes are given. A variety of plots are shown to
illustrate Mathematica's display capabilities, including wiggle-trace plots,
variable-density plots, 3-D plots, and others.
Reservoir Characterization
Reservoir velocity analysis on the Connection Machine (ps 2321K) (src 7176K)
Lumley D. E.
I am developing techniques to perform a detailed reservoir characterization
given 3-D prestack surface seismic data. In this paper,
I develop and implement two velocity analysis algorithms on an 8k
processor Connection Machine CM-2.
The first algorithm performs a weighted semblance stacking velocity analysis,
and is general for 3-D bin geometries. It is heavily I/O bound,
and the inner computational core currently runs at about 120 Mflop/s.
The second algorithm performs a full 3-D prestack time migration velocity
semblance analysis. It is mostly cpu bound and currently runs at about
420 Mflop/s. These results are expected to scale fairly linearly on
a full 64k processor CM-2 to 1 Gflop/s for stacking velocity analysis
and over 3 Gflop/s for prestack time migration velocity analysis.
I tested the algorithm on a marine data set recorded
over a producing gas reservoir in the Gulf of Mexico. This example
shows a variation of at least 100 m/s in migration velocity, or about
500 m/s in interval velocity, in about 700 m distance along the gas reservoir
unit. The estimated velocity variation correlates with AVO bright and dim
spots, suggesting a technique for mapping 3-D spatial reservoir gas saturation
and hydrocarbon pore volume.
Traveltime tomography in azimuthally anisotropic media (ps 325K) (src 269K)
Michelena R. J.
I propose a method of seismic traveltime
tomography in azimuthally anisotropic media consisting of
dipping transversely isotropic layers.
The model used for velocities
is elliptical with variable inclination of the axis of symmetry.
When used with the double elliptic approximation, the method can be
used to fit general transversely isotropic media.
This method is a generalization of conventional tomographic inversion
techniques where the interfaces of the model
are allowed to change their positions and to be eliminated
from the inversion as iterations proceed, which allows
a better estimation of the remaining unknowns.
Ray tracing is performed in anisotropic models.
The technique is tested with cross-well synthetic and field data
where
both strong anisotropy and strong velocity contrasts are present.
Lab measurement of elastic velocities in dry and saturated Massillon Sandstone (ps 116K) (src 206K)
Lumley D., Bevc D., Ji J., and Tálas S.
Lab measurement of physical rock properties, such as seismic compressional
and shear velocities, can be an important link between in situ
measurements of borehole lithology and the information content in
remotely sensed surface seismic data.
We made lab measurements of elastic velocities 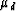 and
and 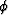 in dry and saturated Massillon Sandstone rock samples.
The rock samples were placed under a uniaxial force of 100 lb distributed over
the core sample end surface area. ¶ and § pulsed waves were transmitted
through the rock sample and first-break arrival times were picked from
¶ and §-mode waveforms. The first-break analysis gives dry rock
¶ and § wave velocities
of
in dry and saturated Massillon Sandstone rock samples.
The rock samples were placed under a uniaxial force of 100 lb distributed over
the core sample end surface area. ¶ and § pulsed waves were transmitted
through the rock sample and first-break arrival times were picked from
¶ and §-mode waveforms. The first-break analysis gives dry rock
¶ and § wave velocities
of 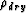 dry = 2918
dry = 2918 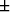 32 m/s and
32 m/s and 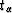 dry = 1731
dry = 1731 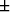 99 m/s,
and water-saturated rock velocities of
99 m/s,
and water-saturated rock velocities of 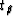 wet = 3380
wet = 3380 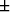 78 m/s and
78 m/s and
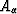 wet = 1744
wet = 1744 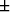 201 m/s, respectively. We also tested Gassmann's
prediction of saturated velocity from the dry rock measurements, and found that
Gassmann's relation gave incorrect and potentially misleading results, on
the order of 20% less than lab measured saturated velocities.
201 m/s, respectively. We also tested Gassmann's
prediction of saturated velocity from the dry rock measurements, and found that
Gassmann's relation gave incorrect and potentially misleading results, on
the order of 20% less than lab measured saturated velocities.
Interpolation
A 3-D local plane-wave interpolation scheme (ps 371K) (src 1207K)
Cole S. and Claerbout J.
Starting from a 2-D interpolation scheme presented elsewhere
in this report, we develop an algorithm for interpolation
of 3-D data. Spatial prediction filters are used to
estimate the apparent dip between pairs of traces.
These dip estimates are combined to give a local estimate
of the true dip in 3-D, which is then used to perform interpolation.
Dealiasing bandlimited data using a spectral continuity constraint (ps 1082K) (src 2168K)
Nichols D.
When aliased data is slant stacked it sums coherently at
multiple locations in the slowness-frequency (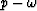 ) domain. Only one of
these locations is the ``true'' location. If the true location can be
distinguished from the aliased locations an unaliased
representation of the data can be computed. The criterion I use
to distinguish between the true dip and the aliased dip is that, for
bandlimited data, the amplitude spectrum at the true dip should be a
locally continuous function of frequency. Once an unaliased
representation of the data has been obtained any slowness domain processing
can be performed before transformation back to the space-time(x-t) domain.
The data can be transformed back to the x-t domain at any
trace spacing to give an dealiased version of the original data.
) domain. Only one of
these locations is the ``true'' location. If the true location can be
distinguished from the aliased locations an unaliased
representation of the data can be computed. The criterion I use
to distinguish between the true dip and the aliased dip is that, for
bandlimited data, the amplitude spectrum at the true dip should be a
locally continuous function of frequency. Once an unaliased
representation of the data has been obtained any slowness domain processing
can be performed before transformation back to the space-time(x-t) domain.
The data can be transformed back to the x-t domain at any
trace spacing to give an dealiased version of the original data.
Seismic trace interpolation beyond spatial aliasing (ps 1351K) (src 4126K)
Zhang L., Claerbout J., and Ji J.
Trace interpolation is often needed for processing spatially-aliased
seismic data. One existing algorithm for trace
interpolation is the linear two-step method. The method
first finds prediction filters from known traces, and then
estimates the missing traces by minimizing the output energy of
the prediction filters. This paper presents a new method for
finding prediction filters from known, spatially-aliased data.
This method has three major advantages over previous methods.
First, it can correctly interpolate data whose dip structure varies
with respect to frequencies. Second, it does not require
the amplitudes of the wavelets along an event to be constant. And third,
it correctly determines prediction filters
even when the data are completely aliased. Examples with synthetic and field
data confirm that this method is superior to the prior algorithms
in handling seriously aliased data.
Trace interpolation by simulating a prediction-error filter (ps 746K) (src 5480K)
Ji J.
By simulating a prediction-error filter using a dip-spectrum,
I devise an interpolation scheme.
The procedure has three stages: (1) First of all, the dips of linear events
in a given data set are estimated from the dip spectrum obtained
from the slant stack. (2) Next, the filters in the (f,x) domain are invented
by putting zeros along the dips picked in the (f,k) spectrum.
(3) Finally, missing traces are found by minimizing the filtered output
in the least square sense.
The advantage of this approach lies in its application to both regularly
and irregularly sampled traces.
Implementation of a simple trace interpolation scheme (ps 762K) (src 5739K)
Bevc D.
A trace interpolation scheme suggested by Muir 1991
is implemented and
tested on real and synthetic data. The algorithm is conceptually simple:
the assumption is made that there is some low-frequency portion
of the data that is not spatially aliased and which
can safely be interpolated. For each trace there is some
relationship between the unaliased low-frequency data and the spatially
aliased high-frequency data. This relationship can be found for each
of the original traces and then used to reconstruct the high-frequency data
on the interpolated traces.
The nonstationarity of seismic data makes it necessary to perform the
interpolation on small windows of data.
The method works well for real and synthetic data when the original data
are uniformly sampled and have an adequate low-frequency component.
DMO and Migration
Finding the amplitudes of migration hyperbolas from the kinematics (ps 255K) (src 1647K)
Abma R. and Claerbout J.
In migration and DMO, the kinematic problem is easier to solve than
the amplitude problem. Where a purely analytical approach is normally
used to obtain the amplitude of a migration operator, we attempt to obtain
amplitude information by combining
an assumption of a flat spectrum
with the kinematical formulation.
This hyperbola whitening is done
with a 2-D prediction-error filter.
This technique is applied to three hyperbolas: a kinematic-only hyperbola,
a amplitude-corrected hyperbola, and an amplitude-corrected hyperbola
with a half-derivative filter.
The results show that the
assumption of a flat spectrum conflicts with the existence of an
evanescent zone, creating unresolved difficulties.
On the imaging condition for elastic reverse-time migration (ps 369K) (src 1109K)
Filho C. A. C.
Migration-based methods have been proposed recently as a solution for
correctly estimating angle-dependent reflectivity in the presence of
complex structures.
I evaluate the use of different imaging conditions for
anisotropic prestack reverse-time migration that aim the estimation
of the reflectivity as a function of the local illumination angle.
Emphasis is given to a particular imaging criterion that generates
four simultaneous images. These images correspond to the in-depth (local)
plane-wave response for P-P, P-S, S-P, and S-S modes and can
be used in a Zoeppritz-based elastic inversion scheme.
DMO after logarithmic stretching (ps 53K) (src 11K)
Schwab M.
DMO stacks seismic offset data by honoring the reflector dips.
This method can be an attractive compromise between computationally expensive
prestack migration and inaccurate NMO. The DMO process implemented here
is accurate
for any constant velocity medium. The algorithm is velocity independent in
the sense that it does not assume a certain velocity value. The DMO step
prepares the data for an NMO step. The subsequent NMO facilitates an
improved velocity analysis and stack, since it does not require a flat
reflector
assumption.
Logarithmic stretching and Fourier transformation along the time axis
reduce the 3D DMO operator to a midpoint and frequency invariant 2D operator.
The duality properties of the Fourier transformation and the band limitation
of our signal allow an efficient representation of the logarithmically scaled
traces.
In this article I present the kinematics of the basic DMO operator.
I outline a program based on logarithmic resampling in temporal frequency,
followed by 2D convolution over constant-frequency planes.
The proposed DMO algorithm is highly parallel and should lend itself to
a very efficient
implementation.
Logarithmic variable transformation (ps 50K) (src 9K)
Schwab M. and Biondi B.
The problem at hand is stretching a time series p(t). The amount of
stretch is to be proportional to time t:
| 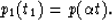 |
(1) |
...
Dip-moveout processing: A tutorial Part 1: DMO basics (ps 354K) (src 307K)
Popovici A. M.
The Dip Moveout correction (DMO) is an intermediate processing
step which when applied together with the Normal Moveout correction
(NMO) transforms a constant-offset section into a zero-offset
section.
There are many benefits to introducing the DMO processing step.
By applying the succession of DMO, NMO, stacking and zero-offset migration
we replace the more expensive sequence of prestack migration
for each offset and stacking.
However the migration to zero-offset is not the only
improvement that DMO delivers
...
Time-to-depth conversion (ps 57K) (src 11K)
Zhang L.
It is well known that, even if correct velocity information is provided,
any conventional time-migration algorithm outputs erroneous images
of subsurface structures whenever overburden
velocities vary laterally. Depth migration has been demonstrated
to be superior to time migration in handling general velocity variations.
However, even today, time migration is still widely used in industry.
Black and Brzostowski (1992) gave two reasons to explain
the continued wide-spread use of time migration. Their first reason
concerns computational costs.
They estimated that depth migration usually requires an order of magnitude
...
Wave-equation extrapolation of land data with irregular acquisition topography (ps 46K) (src 6K)
Bevc D.
Seismic data gathered on land is distorted by
irregular acquisition topography. Most seismic imaging algorithms are applied
to data which is shifted to a planar datum. In regions of mild topography
a static shift is adequate to perform this transformation
Jones and Jovanovich (1985), however as the
necessary shift increases in magnitude, the static approximation becomes
inadequate. In this situation a procedure based on
wave-equation extrapolation is more appropriate than static shift
...
Modeling
Solving the frequency-dependent eikonal equation (ps 251K) (src 1490K)
Biondi B.
The eikonal equation that is commonly used for modeling
wave propagation is frequency independent.
Therefore, it cannot correctly model the propagation
of seismic waves when rapid variations in the velocity
function cause frequency dispersion of the wavefield.
I propose a method for solving a
frequency-dependent eikonal equation, that can be
derived from the scalar wave equation without approximations.
The solution of this frequency-dependent eikonal
is based on the
extrapolation of the phase-slowness function downward along
the frequency axis starting from infinite frequency,
where the phase slowness is equal to the medium slowness.
The phase slowness is extrapolated by
solving a non-linear
partial differential equation using an explicit
integration scheme.
The extrapolation equation contains terms that are functions
of the phase slowness, and terms that are functions of the
ray density.
When the terms that are dependent on the rays are neglected,
the extrapolation process progressively smooths the
slowness model;
this smoothing is frequency-dependent and consistent with the
wave equation.
Numerical experiments of wave propagation through
two simple velocity models show that the solution
of the frequency-dependent
eikonal computed using the proposed method matches the
results of wave-equation modeling significantly
better than the solution of the conventional eikonal
equation.
Elastic modeling in discontinuous media: testing the dynamic response (ps 423K) (src 8600K)
Filho C. A. C.
A simple discontinuous model with known analytical solution
is used to compare the dynamic response of three elastic modeling schemes.
One scheme is based on the Haskell-Thomson propagator-matrix and the
other two are based on finite-differences. One of the finite-difference
schemes follows the traditional discretization of the elastic wave equation
while the other is based on a discretization approach developed
for discontinuous media. Except for a higher dispersion in the
traditional finite-differences, all approaches show a similar behavior at
small angles of incidence. At larger illumination angles, the modified
finite-difference and the propagator-matrix methods are much closer
to the analytical solution than the traditional finite-difference approach.
These results may have a considerable impact in the accuracy of
finite-differences-based inversion schemes whenever the subsurface
geology is better described (within the resolution wavelength of the data)
by a model with sharp interfaces rather than by a smoothly varying model.
3-D and 2-D phase shift plus interpolation and split-step Fourier modeling (ps 973K) (src 1221K)
Popovici A. M.
Migration algorithms based on Fourier methods are naturally parallel.
The modeling algorithm which is the conjugate transpose
of the migration algorithm (or vice-versa)
preserves all the parallel features of the direct (migration)
algorithm.
I implemented two Fourier based modeling algorithms on the
Connection Machine.
Both methods are the
conjugate transpose of two migration algorithms
(Phase Shift Plus Interpolation and Split-Step).
I tested the algorithms on 3-D and 2-D variable velocity models.
I compare both methods considering speed and accuracy.
Kinematic ray tracing in anisotropic layered media: practical details (ps 286K) (src 233K)
Michelena R. J.
I review a procedure to trace rays in layered transversely
isotropic
models with dipping interfaces.
Group velocities are used to propagate the ray across each homogeneous layer
and phase velocities are used
to
find out how a given ray changes its direction
when impinging on an interface.
The equation that relates the ray parameter of the incident
ray with the angle of the emergent
phase at each interface is studied in detail.
Examples of ray tracing in simple models
are shown.
Claerbout
Introduction to Kirchhoff migration programs (ps 288K) (src 6K)
Claerbout J. F.
In the simplest zero-offset Kirchhoff program
(which is very slow) loops may be reordered arbitrarily.
I reorder the code to avoid computing results that lie
off the bottom of mesh and to reuse square roots
thus making the code run much faster.
An example shows that
diffraction followed by migration gives low frequency
amplification.
Spatial aliasing (ps 39K) (src 4K)
Claerbout J. F.
The plane wave model links an axis that is not aliased
with one that might be.
Anti aliasing (ps 445K) (src 30K)
Claerbout J. F.
Field arrays filter spatially.
On dipping arrivals this produces a temporal filtering effect.
To match field arrays,
Kirchhoff operators are designed to antialias with short rectangle
and triangle smoothing functions
whose duration depends on the local trace-to-trace moveout.
Integrals under triangular shaped weighting windows
are rapidly computed from the double integral of the trace.
Each integral is a weighted sum of three values of the double integral,
one from each corner of the triangle.
Complete code is given along with examples.
Nonstationarity and conjugacy: utilities for data patch work (ps 75K) (src 8K)
Claerbout J. F.
I design and explain programs for parceling a planar
data set into an array of patches (small planes) that may overlap.
The conjugate takes the patches and adds them back together
into a data plane.
Because of overlap,
the original data set is not recovered
unless weighting functions are used.
Any weighting function can be used in any patch.
I provide a seamless reconstruction
with code in which you can incorporate any linear operator.
Finally, I code time and space variable 2-D filtering
using invariant filtering in patches,
taking care that filters do not run off the boundaries of each patch
and using triangular weighting functions to merge patches.
Filling data gaps using a local plane-wave model (ps 119K) (src 13K)
Claerbout J. F.
I assemble a utility for trace interpolation assuming
a local monoplanewave model.
In local windows,
many one-point filters are tested with various dips.
These are trivial spatial prediction filters.
These simple filters are easily interpolated leading to data interpolation.
PVI introduces the idea of 2-D prediction-error filters to data interpolation.
The method here reduces that concept to practice in an elementary way.
This method is the first step of a family of inverse methods
that I am developing.
Information from smiles: mono-plane-annihilator weighted regression (ps 658K) (src 12K)
Claerbout J. F.
An interpreter looking at a migrated section containing
two dips in the same place knows that something is wrong.
To minimize the presence of multiple dipping events in the same place,
we can design a rejection filter
to remove the best fitting local plane.
This is called a LOMOPLAN (LOcal MOno PLane ANnihilator).
The output of a LOMOPLAN contains only other dips
so minimizing that output should enable us
to improve estimation of model parameters and missing data.
Although the LOMOPLAN concept applies to models, not data,
experience shows that processing field data with a LOMOPLAN
quickly identifies data quality problems.
A LOMOPLAN
for adequately sampled 3-D data is
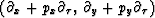 which has two outputs, both of which should be minimized.
which has two outputs, both of which should be minimized.
Crossline regridding by inversion (ps 554K) (src 14K)
Claerbout J. F.
I sketch the regression strategy I am planning for crossline regridding
and interpolation by iterative migration.
Miscellaneous
On the validity of a variable velocity acoustic wave equation (ps 45K) (src 64K)
Lumley D. E.
I consider the validity conditions for the variable velocity acoustic wave
equation (1). This equation is sometimes used in
geophysical applications
of seismic wave propagation, imaging and inversion, without regard to the
specific assumptions underlying its derivation or the validity of its use
as a practical approximation. To gain some insight into these validity
conditions, I carry out the necessary mathematical analysis to
further illuminate the subject. To apply my results to seismic data,
one has to assume that the Earth is a linear isotropic non-viscous fluid,
...
Random sequences: a review (ps 48K) (src 9K)
Muir F.
Notions of randomness are not new in exploration seismology -
white noise has been with us since the genesis of digital
signal processing - but it is likely that they will find increasing
use as we move from a deterministic to a probabilty basis for seismic
data processing.
In this Short Note I describe the desirable properties of
computer-generated random sequences, and present some simple
type algorithms.
...
Automatic differentiation (ps 70K) (src 544K)
Karrenbach M.
In the past the development of automatic differentiation algorithms was driven
by the need for the efficient evaluation of exact derivative values. In
atmospheric and oceanographic sciences, the need for exact derivative values
is particularly great, because researchers in these areas
use more and more sophisticated first- and higher-order
derivatives in their model description.
Although automatic differentiation tools have so far not been widely used in exploration
geophysics, they offer possibilities
in non linear optimization, complex algorithms, and statistical analysis.
...
How to use cake with interactive documents (ps 48K) (src 8K)
Claerbout J. F.
My experience with maintaining 300 illustrations
has been distilled to two pages of cake rules.
Each directory has a cakefile
containing a list (FIGLIST) of buildable figure names.
All figures can be built with the command cake figures
and removed with cake burn.
Precious figure files (ones not considered replaceable)
are named NAME.save.
Interactive figures are launched by the target NAME.idoc.
A tour of SEPlib for new users (ps 93K) (src 750K)
Dellinger J. and Tálas S.
SEPlib is a data-processing software package developed
at the Stanford Exploration Project.
Many researchers at universities and oil companies would find SEPlib
extremely useful if they could only get over the initial hump of learning
how SEPlib programs are used.
By working through several illustrative examples
this document attempts
to painlessly introduce novice users to the fundamental SEPlib concepts
they will need to understand the available SEPlib self-documentation and
manual pages.
Concepts covered include
self-documenting programs,
history files and data files,
SEPlib-style pipes,
command-line and history-file ``getpar'' parameters,
auxiliary input and output,
and how to use some of the more useful SEPlib utilities.
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)




Next: About this document ...
Up: Table of Contents
Stanford Exploration Project
11/18/1997
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) (ps 850K) (src 1484K)
(ps 850K) (src 1484K)
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)