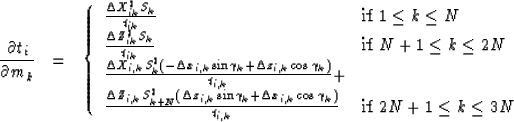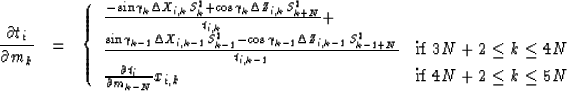Next: About this document ...
Up: Michelena: Anisotropic tomography
Previous: ACKNOWLEDGMENTS
- Byun, B. S., 1982, Seismic parameters for media with elliptical
velocity dependencies: Geophysics, 47, 1621-1626.
- Chapman, C. H. and Pratt, R. G., 1992, Traveltime tomography in
anisotropic media: Theory: Geophys. J. Intl., 109, 1-19.
- Dellinger, J. and Muir, F., 1991, The double elliptic
approximation in the group and phase domains: SEP-70, 361-366.
- Gill, P. H., Murray, W., and Wright, M. H., 1981,
Practical Optimization: Academic Press.
- Harlan, W. S., 1989, Tomographic estimation of seismic velocities
from reflected raypaths: presented at the 59th Ann. Internat. Mtg., Soc. Expl.
Geophys.
- Harris, J., M., 1988, Cross-well seismic measurements
in sedimentary rocks: presented at the 58th Ann. Internat, Mtg.,
Soc. Expl. Geophys.
- Lazaratos, S. K., Rector, J. W., Harris, J. M. and
Van Schaack, M., 1991, High resolution imaging with cross-well
reflection data:
presented at the 61st Ann.
Internat. Mtg., Soc. Expl. Geophys.
- Lee, M.,W.,1990,
Traveltime inversion using transmitted waves of offset vertical seismic
profiling data: Geophysics, 55, 1089-1097.
- McMechan, G.A., 1983,
Seismic tomography in boreholes:
Geophys. J. Roy. Astr. Soc., 74, 601-612.
- Michelena, R. J., 1990, Traveltime inversion with constraints:
STP-1, paper H.
- Michelena, R. J., 1992,
Kinematic ray tracing in anisotropic layered media: SEP-73.
- Michelena, R. J., Muir, F. and Harris, J. M., 1992,
Anisotropic traveltime tomography: submitted for publication in
Geophysical Prospecting.
- Miller, D. E., and Chapman, C. H., 1991, Incontrovertible
evidence of anisotropy in cross-well data:
presented at the 61st Ann.
Internat. Mtg., Soc. Expl. Geophys.
- Muir, F., 1990, A modified anisotropic system: SEP-67,
41-42.
- Nolet, G., 1987, Seismic wave propagation and seismic
tomography, in Nolet, G., Ed., Seismic tomography:
D. Reidel Publ. Co., 1-23.
- Onishi, M., and Harris, J., M., 1991, Anisotropy from
head waves in cross-well data:
presented at the 61st Ann.
Internat. Mtg., Soc. Expl. Geophys.
- Pratt, R. G., Chapman, C. H., 1992, Traveltime tomography in
anisotropic media: application: Geophys. J. Intl.,109, 20-37.
- Raikes, S., 1991, Shear-wave characterization of the BP
Devine test site, Texas:
presented at the 61st Ann.
Internat. Mtg., Soc. Expl. Geophys.
- Van Trier, J., 1988, Migration velocity analysis using geological
constraints: presented at the 58th Ann. Internat. Mtg., Soc. Expl.
Geophys.
The expression for the ray velocity in a medium with elliptical
velocity dependency is given by the expression
| 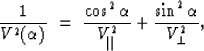 |
(9) |
where  is the ray angle measured from the axis of symmetry
(positive counterclockwise)
and
is the ray angle measured from the axis of symmetry
(positive counterclockwise)
and 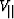 and
and 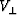 are the velocities in the directions
parallel and perpendicular to the axis of symmetry
(Figure A-1-a).
When the axis of symmetry is vertical, the angle that measures
the direction of propagation of the ray with respect to the vertical
is the same as the group velocity angle.
are the velocities in the directions
parallel and perpendicular to the axis of symmetry
(Figure A-1-a).
When the axis of symmetry is vertical, the angle that measures
the direction of propagation of the ray with respect to the vertical
is the same as the group velocity angle.
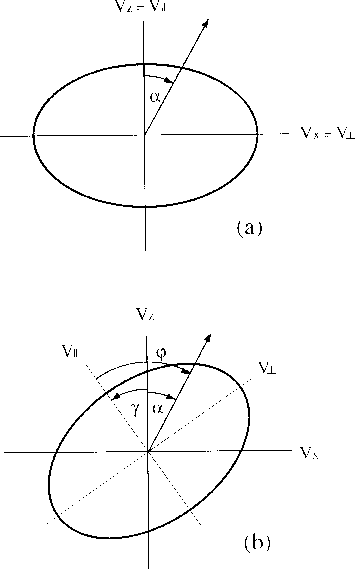
When the axis of symmetry is rotated an angle 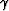 (Figure A-1-b),
the expression for the ray velocity becomes (for the same
ray direction):
(Figure A-1-b),
the expression for the ray velocity becomes (for the same
ray direction):
| 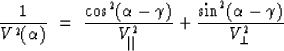 |
(10) |
tilted-ellipses
Figure 11 Ray velocity as a function of direction in an elliptically anisotropic
medium: (a) Axis of symmetry vertical (ray angle = group velocity angle).
(b) Axis of symmetry tilted (ray angle =  ; group velocity angle =
; group velocity angle =
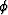 ).
).

where 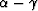 is the angle from the axis of symmetry to the
ray (group velocity angle).
is the angle from the axis of symmetry to the
ray (group velocity angle).
If the ray travels a distance d
between two points (Figure 1),
| 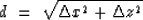 |
(11) |
the corresponding traveltime t is
| 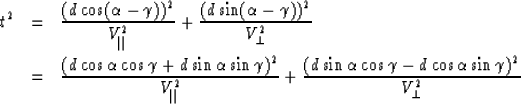 |
(12) |
| |
To further simplify this equation we need to know the values
of 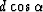 and
and 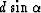 . In order to do this, we
need to be careful about the sign of
. In order to do this, we
need to be careful about the sign of  (clockwise
or counterclockwise) for the
given ray direction. We also need to be careful about the sign of
(clockwise
or counterclockwise) for the
given ray direction. We also need to be careful about the sign of
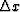 and
and 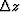 .It turns out that regardless of how the signs of these quantities
are defined (as long as they are consistent)
the final
expression for t2 is always, as expected, the same. The result
is
.It turns out that regardless of how the signs of these quantities
are defined (as long as they are consistent)
the final
expression for t2 is always, as expected, the same. The result
is
| 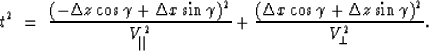 |
(13) |
This is the expression for the traveltime of a ray that travels
between two points separated by a distance
d in an homogeneous elliptically anisotropic
medium with axis of symmetry forming an angle 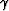 with
the vertical. This equation is the heart of the inversion procedure
proposed in this paper.
with
the vertical. This equation is the heart of the inversion procedure
proposed in this paper.
In this appendix, I show the expressions for the partial
derivatives of the traveltime ti
(equation (5))
with respect to the model parameters mk, where mk
is a component of the vector m:
First, the derivatives with respect to the interval parameters
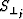 ,
, 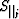 and
and 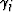 (
(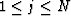 ):
):
Note that for the interval
parameters
the derivatives with respect to the jth variable depend only
upon the properties of the jth layer.
The derivatives of the traveltime with respect to
the boundary parameters (aj and bj), depend on the properties
of the medium above and below that boundary, as follows:
Since the traveltime ti is not affected by the position of the
top boundary, 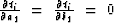 .
.
When a ray travels horizontally, only the first
N components of the vector of partial derivatives
are non zero. For the forward modeling
this is not problem and it
simply means that the horizontal
component of the velocity is the only parameter that affects the traveltime
of a horizontally traveling ray.
Problems arise, however, when we try to
invert these traveltimes because
there are infinite combinations of the other parameters that
satisfy the data equally well (null space).
This translates into instability
of the inversion procedure. For these reason, this
inversion
does not use rays that travel exactly along the horizontal.
After making the appropriate simplifications in the above equations for the
case of isotropic media, it results a set of equations similar to
the ones obtained by Lee (1990). Note two misprints in Lee's equations.





Next: About this document ...
Up: Michelena: Anisotropic tomography
Previous: ACKNOWLEDGMENTS
Stanford Exploration Project
11/18/1997
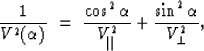
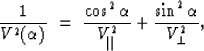
![]() (Figure A-1-b),
the expression for the ray velocity becomes (for the same
ray direction):
(Figure A-1-b),
the expression for the ray velocity becomes (for the same
ray direction):
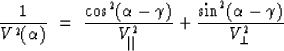
![]() is the angle from the axis of symmetry to the
ray (group velocity angle).
is the angle from the axis of symmetry to the
ray (group velocity angle).
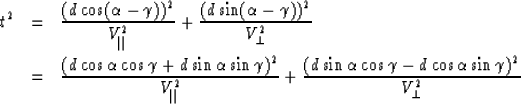
![]() and
and ![]() . In order to do this, we
need to be careful about the sign of
. In order to do this, we
need to be careful about the sign of ![]() (clockwise
or counterclockwise) for the
given ray direction. We also need to be careful about the sign of
(clockwise
or counterclockwise) for the
given ray direction. We also need to be careful about the sign of
![]() and
and ![]() .It turns out that regardless of how the signs of these quantities
are defined (as long as they are consistent)
the final
expression for t2 is always, as expected, the same. The result
is
.It turns out that regardless of how the signs of these quantities
are defined (as long as they are consistent)
the final
expression for t2 is always, as expected, the same. The result
is
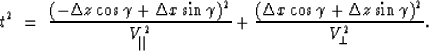
![]() ,
, ![]() and
and ![]() (
(![]() ):
):