Next: CONCLUSIONS
Up: Abma: The seismic data
Previous: Reconstruction Problems with Seismic
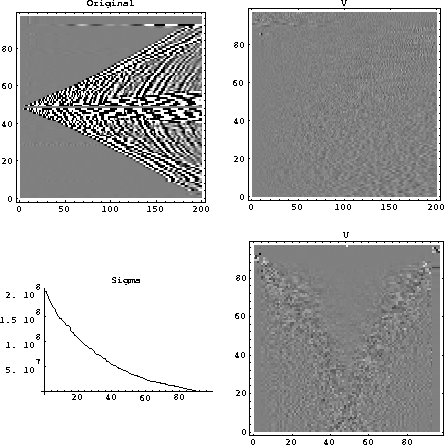
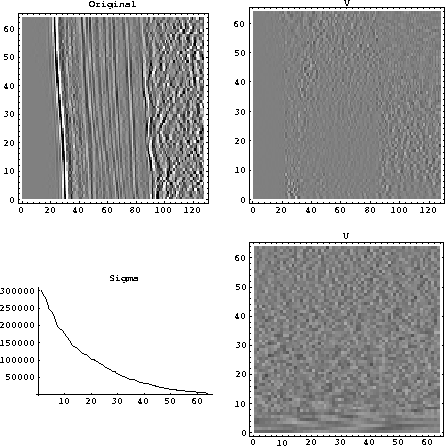
The first example of decomposing a seismic record is the shot record shown
in Figure 8. The plot of 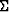 shown in the figure shows the
singular values decreasing slowly compared to the those in the photographic
case.
The U matrix also shows significant detail on the vectors corresponding
to the smaller singular values. The reconstructions of the shot gather
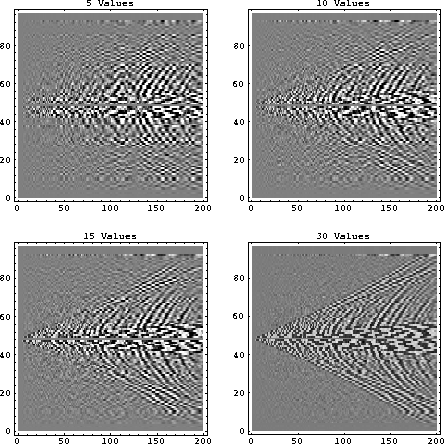
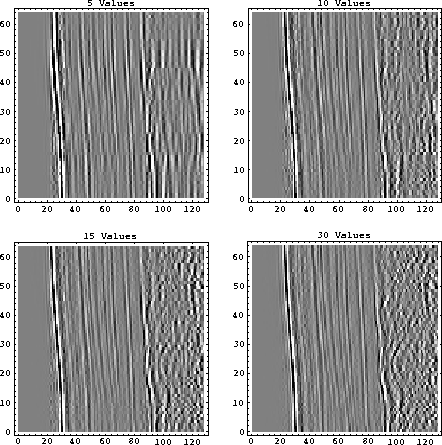
using a only few of the larger singular values are shown in Figure 9. When
only five singular values are used to reconstruct the shot gather, much of the
dipping energy is lost, but as more singular values are used, the steeper
dips gradually reappear. Even while using 30 singular values, the
shot gather is poorly reconstructed. Most of the high amplitude events
have reappeared, but the small details are washed out, and noise has
corrupted the low amplitude background above the first breaks.
shown in the figure shows the
singular values decreasing slowly compared to the those in the photographic
case.
The U matrix also shows significant detail on the vectors corresponding
to the smaller singular values. The reconstructions of the shot gather
using a only few of the larger singular values are shown in Figure 9. When
only five singular values are used to reconstruct the shot gather, much of the
dipping energy is lost, but as more singular values are used, the steeper
dips gradually reappear. Even while using 30 singular values, the
shot gather is poorly reconstructed. Most of the high amplitude events
have reappeared, but the small details are washed out, and noise has
corrupted the low amplitude background above the first breaks.
shotsvd
Figure 8
A shot gather and its decomposition. Notice the slow decrease in the size
of the singular values and the structure evident in the U matrix.

shotreci
Figure 9
The shot gather reconstructed using 5, 10, 15, and 30 singular values.
Events with low dips are reconstructed with the first few singular values,
and the higher dips appear with the smaller singular values added later.

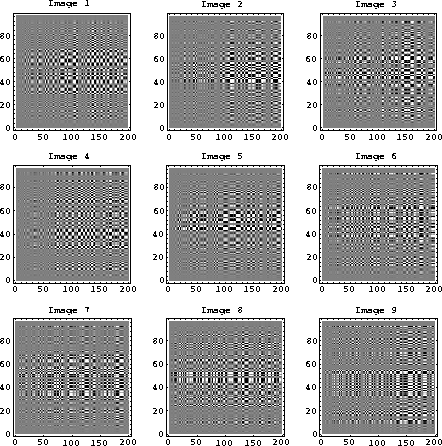
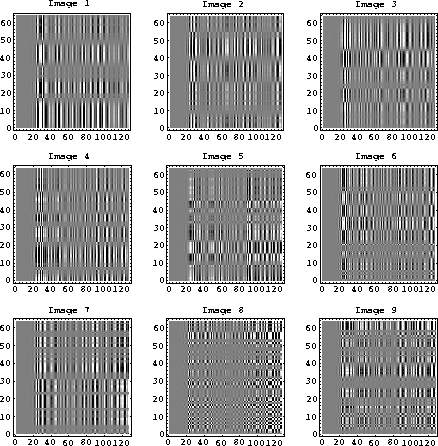
Figure 10 has been included here to give the reader an idea of what the
images corresponding to the first few singular values of the
shot gather look like. Here vertical and horizontal patterns make
it obvious that the images are the
outer products of two vectors.
The first few images in Figure 10
have the energy concentrated about the central
portion of the image. This corresponds roughly to the reconstructions
shown in Figure 9, where the flat data in the center is reconstructed
first. The steep-dip data in the outer traces associated
with the smaller singular values are imaged with the later, smaller
singular values.
shotiter
Figure 10
The images of a shot gather associated with the first nine singular values.
Here it becomes obvious that the images are constructed from the outer
product of two vectors.

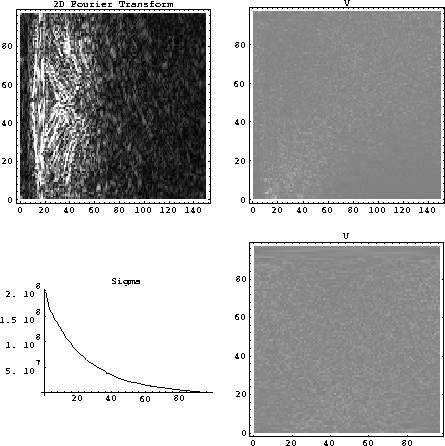
In an attempt to simplify the input to the singular value decomposition,
a two-dimensional Fourier transform was applied to the shot record. The
transform, as seen in Figure 11, shows that much of the energy is
concentrated in the lower frequency range. While dips are still present,
the dips are smaller than those in the original shot gather. It is
interesting to see that the plot of the singular values appears to be
similar to the plot of the singular values of the original shot gather
shown in Figure 8. Although much
of the detail in the U and V matrices is lost
because the plots show the absolute value of the complex numbers, the
U and V matrices appear much simpler than the U and V matrices of the
original shot gathers.
2dfftsvd
Figure 11 The two-D Fourier
transform of the shot gather
and its decomposition. Notice the slow decrease in the size
of the singular values and compare these singular values
to the singular values shown
in Figure 8.

More success compressing stacked datasets is expected, since these
data contain fewer high-amplitude steep-dip events than
typical shot gathers.
The stack shown in
Figure 12 contains gently sloping events
below the water bottom and more complex structures deeper in the section.
The plot of the singular values
shows a pattern similar to the singular values of the
shot gather, which is surprising, since the dips are smaller and the
dipping events are of lower
amplitude in the
stacked case.
When the original data is reconstructed from the stack's
decomposition using the first few singular values, discontinuities can
be seen in the first few reconstructions shown in Figure 13. The steeper
dips missing on the first few reconstructions
do not appear until the last reconstruction using 30 singular values.
stksvd
Figure 12
A stack and it's decomposition.
While the stack appears simpler than the shot gather shown in Figure 8,
the slow decrease of the singular values is similar.

stackreci
Figure 13
The stack reconstructed using 5, 10, 15, and 30 singular values.
Notice the discontinuities in the shallow zone
and the lost diffraction tails in
the deeper zone for the reconstructions using 5 and 10 values.

Figure 14 shows the images associated with the first few singular values
and gives some insight into the discontinuities seen in the reconstructions
shown in Figure 13. The reflections are broken up into events
consisting of alternating polarities with spatial periods that generally
decrease
as the size of the singular values decrease. As more singular values
are used, more detail is seen in the reconstruction.
stkiter
Figure 14
The stack images associated with the first nine singular values.

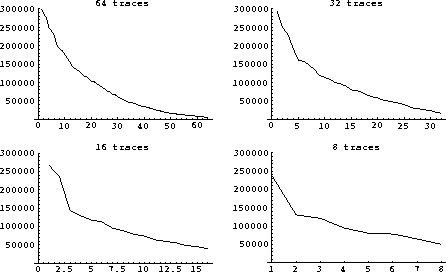
While it might be hoped that increasing or decreasing the number of traces
put into the singular value decomposition might change the trend of the
singular values, this effect is not seen with the stack image.
Figure 15 shows the singular values for various numbers
of traces from the stack in Figure 12. The slow decrease in amplitude
of the singular values is similar for all these cases.
stackvar
Figure 15
Sizes of the singular values using 64, 32, 16, and 8 traces of a stack image.
The slow decrease in amplitude is similar for these cases.






Next: CONCLUSIONS
Up: Abma: The seismic data
Previous: Reconstruction Problems with Seismic
Stanford Exploration Project
11/18/1997
![]() shown in the figure shows the
singular values decreasing slowly compared to the those in the photographic
case.
The U matrix also shows significant detail on the vectors corresponding
to the smaller singular values. The reconstructions of the shot gather
using a only few of the larger singular values are shown in Figure 9. When
only five singular values are used to reconstruct the shot gather, much of the
dipping energy is lost, but as more singular values are used, the steeper
dips gradually reappear. Even while using 30 singular values, the
shot gather is poorly reconstructed. Most of the high amplitude events
have reappeared, but the small details are washed out, and noise has
corrupted the low amplitude background above the first breaks.
shown in the figure shows the
singular values decreasing slowly compared to the those in the photographic
case.
The U matrix also shows significant detail on the vectors corresponding
to the smaller singular values. The reconstructions of the shot gather
using a only few of the larger singular values are shown in Figure 9. When
only five singular values are used to reconstruct the shot gather, much of the
dipping energy is lost, but as more singular values are used, the steeper
dips gradually reappear. Even while using 30 singular values, the
shot gather is poorly reconstructed. Most of the high amplitude events
have reappeared, but the small details are washed out, and noise has
corrupted the low amplitude background above the first breaks.