DATA COMPRESSION WITH THE SINGULAR VALUE DECOMPOSITION

A traditional method of compressing images using the singular value decomposition was a reasonable technique to consider for seismic data compression. This method reproduces most photographic images well and allows a significant storage reduction. It is based on simple ideas and readily available software.

The singular value decomposition is based on decomposing a matrix into two matrices, U and V, and a vector, $\Sigma$, containing scale factors called singular values. This decomposition of a matrix A is expressed as

$$A = U \Sigma V^t$$

Each singular value in $\Sigma$ corresponds to an single two-dimensional image built from a single column in U and a single row in V. The reconstructed image is the sum of each partial image scaled by the corresponding singular value in $\Sigma$.

The key to compressing an image is recognizing that the smallest singular values and their corresponding images should not significantly contribute to the final image. By ignoring the smallest singular values along with the columns in U and the rows in V that these singular values multiply, the original image should be accurately reconstructed from a dataset much smaller than the original matrix. When more than half these singular values are ignored, the parts of the U and V matrices required to reconstruct the image are smaller than the original image. If only a few singular values are needed, a small fraction of the original U and V matrices is needed to reconstruct the image, and the storage cost is cut significantly.

The reconstruction of compressed images while ignoring small singular values is illustrated by decomposing a photograph with the singular value decomposition and then reconstructing it with the largest singular values. Figure 1 shows the original image, the U and V matrices, and the singular values in $\Sigma$, labeled sigma in the plot. Figure 2 shows the reconstruction of the image using first 5, 10, 15, and 30 singular values. Notice that 30 singular values reconstruct an image that is difficult to distinguish from the original. 30 singular values out of 276 produces an excellent compression ratio.

 

stevedec Figure 1 A photograph and its decomposition. Notice the sharp drop in the magnitudes of the singular values shown in Sigma. Also notice the low frequency data in the lower part of the U and V matrices.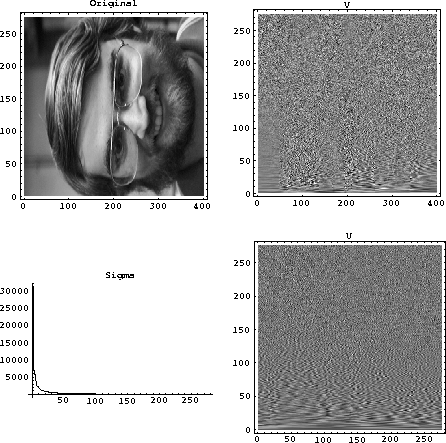

 

steveiter Figure 2 Reconstructed photographs using 5, 10, 15, and 30 singular values. The reconstruction using 30 singular values is practically identical to the original.