Going to the (g1',g2') domain

There are two ways to go to (g1',g2') domain, an indirect and a direct one. The indirect way is to map from (T,1/V_nmo²) to (g1',g2') by including the shear V_water². The result is shown in Figure 3a. Figure 3b is its autocorrelation. This figure shows that the waterbottom multiples and peglegs are periodic in this new Abelian group domain, and the period is constant from trace to trace.

 

SynAbelian
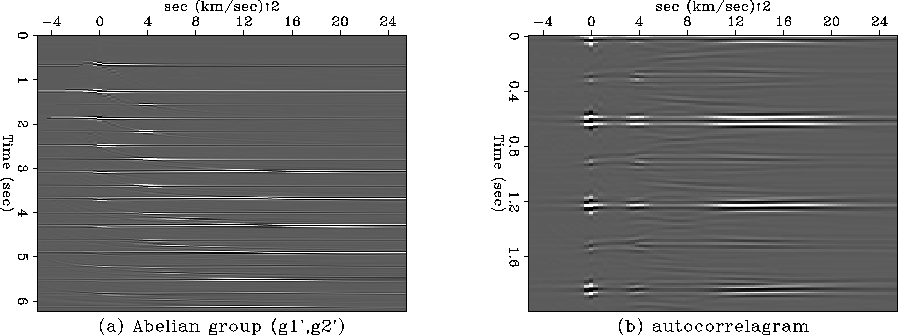
Figure 3 (a) is the Abelian group attributes (g1',g2'), (b) is its autocorrelogram. Water-related reverberations are periodic and lie directly under each other on the g1'=T axis.

We can apply gapped predictive deconvolution on this (g1',g2') in Figure 3a. Conjugate mapping all the way from the deconned Abelian group back to the space-time domain gives the water-related reverberations attenuated section.

Two problems with this mapping are that it requires two more (forward and conjugate via (T,1/V_nmo²) ) mappings, while the amplitude in the (g1',g2') domain is less regular than in the second method described below. So we move on to the second mapping method, a direct one.

The other way to go to (g1',g2') is to do velocity transform mapping directly from the space-time domain. The conjugate mapping from (g1',g2') to material parameters consists of:

1.

T = g1'

2.

V_nmo² = g2'/g1' + V_water².

Considering the velocity uncertainty, for a point in (g1',g2') domain, we use also its left and right neighbors along the g2' axis to invert for material parameters, yielding a T, and three velocities squared. We apply velocity transform by NMO Kirchhoff summation over the hyperbola strip defined by the three velocities squared. The weight given to each summing element is defined by a triangle weighting function, an approximate to a Gaussian function (Jedlicka, 1989). The apex of the triangle is at the NMO time of the median velocity squared. The area under the triangle is $1/ \sqrt{T}$,i. e., we are honoring the 2-D Green's function. The result of summation gives the value at the corresponding point in (g1',g2') domain. The conjugate mapping is the spraying out of the point value in (g1',g2') domain into the NMO hyperbola strip Kirchhoff trajectory in space-time domain (Claerbout, 1991). One caution is that the coordinate g2'=0 must be sampled because it directly samples the water bottom multiples.

The problem with this velocity transform mapping method arises from the different velocity sensitivity in the relation V_nmo² = g2'/g1' + V_water² between shallow and deep parts. When g1'=T is small, a small change in g2' results in a big change in V_nmo². We discard the negative V_nmo² as computed. As a result, the velocity is coarsely sampled at the shallow part, whereas the velocity is densely sampled at the deep part. We apply a weighting function 1/V_nmo² to balance between the number of small and large velocity values used, and to underweight the ridiculously high velocities as computed at the shallow part. And because the 2-D Green's function favors the near-offset strongly, after conjugate inverse velocity transform, the far offset data is attenuated. We include an extra weighting function $1/ \cos^2\theta$, where $\cos\theta$ is the Kirchhoff obliquity factor. From our experiences, the results are acceptable when T>0.3 second.