




Next: About this document ...
Up: Schwab & Biondi: Log
Previous: ADVANTAGES
- Bolondi, C. D., Loinger, E., and Rocca, F., 1982, Offset continuation of seismic sections: Geophysical Prospecting, 30, 813-828.
-
- Forel, D., and Gardner, G. H. F., 1988, A three dimensional perspective on two-dimensional dip moveout: Geophysics, 53, 604-610.
-
- Notfors, C. D., and Godfrey, R. J., 1987, Dip moveout in the frequency-wavenumber domain: Geophysics, 52, 1718-1721.
-
The time stretch (1) amounts to time stretch
proportional to time:
| 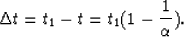 |
(7) |
The logarithmic resampling is defined by:
| 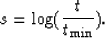 |
(8) |
After logarithmic variable transformation from t to s
the time stretch of equation (1) and
(A-1) is:
| 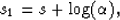 |
(9) |
| 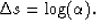 |
(10) |
Having Fourier transformed the time series p'(s) this constant shift
translates to a complex scaling:
| 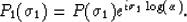 |
(11) |
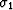 denotes the
denotes the  stretched variable of the
stretched variable of the 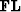 domain.
domain.
After Fourier transformation from variable t to 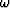 the original stretch relation (1) becomes
the original stretch relation (1) becomes
| 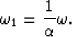 |
(12) |
After logarithmic transformation (A-2) of the frequency trace
we find relationships equivalent to equation (A-3)
and (A-4):
| 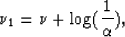 |
(13) |
| 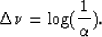 |
(14) |
 describes the new variable in the logarithmic domain.
An additional Fourier transformation allows us
to express the intended
time stretch as a simple scaling (4) of the transformed trace.
describes the new variable in the logarithmic domain.
An additional Fourier transformation allows us
to express the intended
time stretch as a simple scaling (4) of the transformed trace.
We want to map our input trace onto a logarithmic mesh. How many
samples do we need in the logarithmic domain?
According to equation (A-2) the relation between interval
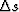 and
and 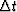 is:
is:
| 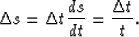 |
(15) |
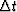 is the sampling interval for which the time trace is properly
sampled.
is the sampling interval for which the time trace is properly
sampled. 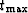 is the maximum time of p(t). At
is the maximum time of p(t). At 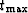
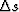 is at a minimum:
is at a minimum:
| 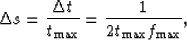 |
(16) |
where 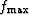 is the Nyquist frequency corresponding to
is the Nyquist frequency corresponding to 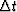 .The number of sample points in the log domain has to be
.The number of sample points in the log domain has to be
| 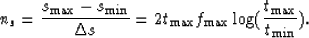 |
(17) |





Next: About this document ...
Up: Schwab & Biondi: Log
Previous: ADVANTAGES
Stanford Exploration Project
11/18/1997
![]() the original stretch relation (1) becomes
the original stretch relation (1) becomes
![]() and
and ![]() is:
is: