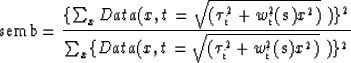
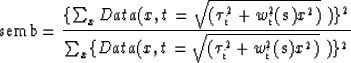 |
(4) |
This objective function measures the quality of a CMP gather stack by using
semblance as a quality measure. Semblance is a nonlinear function of the input parameters, the interval slowness ![]() . In algorithmic terms we can write:
. In algorithmic terms we can write:
for each zero-offset time
![]() {
calculate stacking slowness wi (a)
calcluate moveout curve (b)
calculate semblance
{
calculate stacking slowness wi (a)
calcluate moveout curve (b)
calculate semblance ![]() (c)
}
add up all semblance values
(c)
}
add up all semblance values
A subroutine (Appendix A) can be written that combines all these three steps. In order to see how we can use automatic differentiation, let's look at a subroutine for step (a):
subroutine rmsv(nt,slowint,rms,dt) #ONSTRUCT D(RMS)/D(SLOWINT) IN JACOB(NT,NT) integer nt real slowint(nt) real dt real rms(nt) integer itreal sum,tau real jacob
do it=1,nt { sum = 0. do j=1,it { sum = sum + dt/(slowint(j)*slowint(j)) } tau = it*dt rms(it) = sqrt ( tau / sum )
}
# return stacking velocities rms
return end
This subroutine calculates the RMS slowness from a given interval slowness
model. The second line in the routine is a keyword construct that tells the
preprocessor that we want to calculate the Jacobian of the rms-slowness
model (dependent variable) with respect to the interval slowness model
(independent variable). The velocity model is a taken for only one CMP gather
and constant velocity, just to illustrate the process of automatic differentiation.
The preprocessor produces a subroutine in Fortran77 that
simultaneously evaluates the RMS velocity function and calculates the Jacobian.
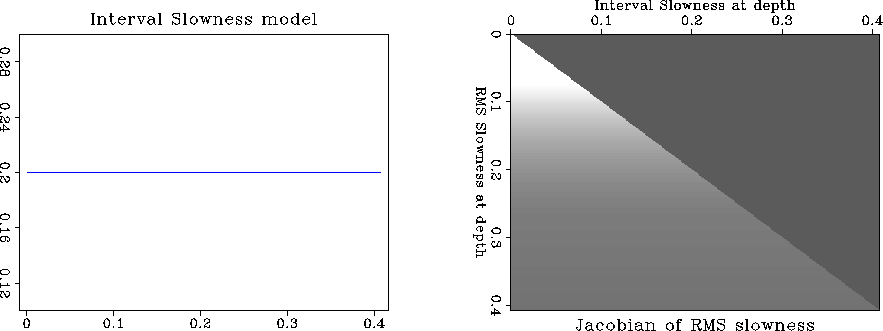
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the interval slowness model and the associated Jacobian for the RMS
velocity model. The calculation is accurate to machine precision. We see
that the Jacobian has values only below the diagonal, because an
RMS slowness value at
shows the interval slowness model and the associated Jacobian for the RMS
velocity model. The calculation is accurate to machine precision. We see
that the Jacobian has values only below the diagonal, because an
RMS slowness value at ![]() does not depend on interval slowness
values below the point
does not depend on interval slowness
values below the point ![]() .
As we can see, the automatic differentiation works well on that piece of
the algorithm. The calculation for step (b) proceeds successfully.
.
As we can see, the automatic differentiation works well on that piece of
the algorithm. The calculation for step (b) proceeds successfully.
 |