




Next: Interpolation
Up: THREE STEP INTERPOLATION
Previous: Dip picking
In the case of randomly missing traces in regularly sampled data,
a prediction-error filter cannot be found.
This section explains an alternative way to find a filter
whose spectrum is the inverse of the given data's spectrum.
If there exist several linear events in a data set, the zeros which were
found by the prediction-error filter would locate along the dips
in the spectrum.
If we know the dips of the events, therefore, we can simulate
the prediction-error filter by putting zeros along the dips in the spectrum.
Suppose we have N plane waves and each dip is pj, j=1,...,N,
respectively.
For each frequency 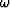 , then, N zeros along the wavenumber
are determined as follows :
, then, N zeros along the wavenumber
are determined as follows :
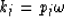
and the corresponding zeros are
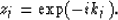
From those zeros, the prediction-error filter for each 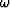 is determined
in the form of the Z transform like
is determined
in the form of the Z transform like
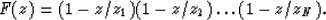





Next: Interpolation
Up: THREE STEP INTERPOLATION
Previous: Dip picking
Stanford Exploration Project
11/18/1997
![]() , then, N zeros along the wavenumber
are determined as follows :
, then, N zeros along the wavenumber
are determined as follows :
![]()
![]()
![]()