Some fundamental data-manipulation programs

By this time you have learned many useful things, but as you are most probably a geophysicist or similar data-crunching creature, you may want to see something more ``exciting'' than just different displays. What about one of the SEP's favorite inverse operations, interpolation? Sounds much more fascinating than those boring displays, doesn't it?

We hope that you are already getting somewhat familiar with SEPlib, so from now on we will not explain all the programs in depth as we did before. Most of the programs are self-explanatory in these examples, and you should not forget about their self documentation (just type the name of the program). So let's start, and good luck!

Start by subsampling the data using Window:

Window < Txx.H j1=2 > Txx_sub.H

This decimates the 1 (time) axis by a factor of 2.

Now suppose we accidentally lost the original data and only had the subsampled version left. If the original data was sufficiently oversampled, we should be able to recover the original by transforming to the Fourier domain, padding, and transforming back. Can we perform this sequence using only available SEPlib utilities?

The Fourier transform utility, ``Ft3d'', demands complex input (it will barf with ``Ft3d: esize must be 8'' if it doesn't get it), so we first convert from Real to Complex using Rtoc. Then we can use Ft3d to do the Fourier transform, with a command-line parameter to tell it we only want to transform over the 1 axis:

Rtoc < Txx_sub.H | Ft3d sign1=1 > Txx_Fft.H

You may enjoy examing a plot of Complex absolute value in the frequency domain:

Cabs < Txx_Fft.H | Wiggle | Tube

Now we pad from 512 back to 1024 points, inverse Fourier-transform, take the real part, make a Wiggle plot, and plot it (whew)!

Pad < Txx_Fft.H n1=1024 | Ft3d | Real | Wiggle par=plotpar | Tube

(We didn't have to tell Ft3d what to do because it looks at the parameters from its last run preserved in the history file, and by default does the inverse.) And the resulting plot is... JUNK!

Well, of course. ``Pad'' is a stupid program that just appends enough zeroes onto the end of a given axis to make a dataset of the requested size. That's fine for some applications, but not for this one. To do the job right we have to separate out the positive frequencies, negative frequencies, DC, and Nyquist and make sure they all end up in the right places. Zero frequency is in slot 0. We have 512 frequency points, so the positive frequencies must be in slots 1 to 255, the Nyquist is in slot 256, and the negative frequencies are in slots 257 to 511. (Almost all SEPlib programs use C numbering notation, not FORTRAN numbering notation... arrays start with element 0, not 1.)

Let's separate them all out.

Window < Txx_Fft.H n1=1 f1=0 squeeze=n > DC.H
Window < Txx_Fft.H n1=255 f1=1 squeeze=n > Pos.H
Window < Txx_Fft.H n1=1 f1=256 squeeze=n > Nyquist.H
Window < Txx_Fft.H n1=255 f1=257 squeeze=n > Neg.H

(If the 1 axis on output would have length 1, Window by default helpfully swaps it around and makes it the 2 axis. For this case it is not helpful. The ``squeeze=n'' option prevents this.)

The Nyquist has to go in twice, so we need to divide it by two:

Add Nyquist.H scale=.5 > Nyquisto2.H

And finally we put it back together with the padding in the middle, and bring it back to the time domain:

Merge axis=1 space=n DC.H Pos.H Nyquisto2.H | Pad > Junk n1=768
Merge axis=1 space=n Junk Nyquisto2.H Neg.H > Txx_Fft2.H
Ft3d < Txx_Fft2.H | Real > Junk
Add Junk scale=1.414213562 > Txx_resamp.H
Rm Junk DC.H Pos.H Nyquisto2.H Neg.H Txx_Fft.H

(Merge by default helpfully inserts a zero trace between merged blocks, so you can see where the boundaries are. ``space=n'' turns this off. We have to rescale by $\sqrt{2}$to take care of the differing FFT normalizations.)

Compare the original and reconstructed data by doing

Cat Txx.H Txx_resamp.H | Wiggle par=plotpar | Tube

As you (hopefully) can see, we appear to have recovered the original dataset exactly.

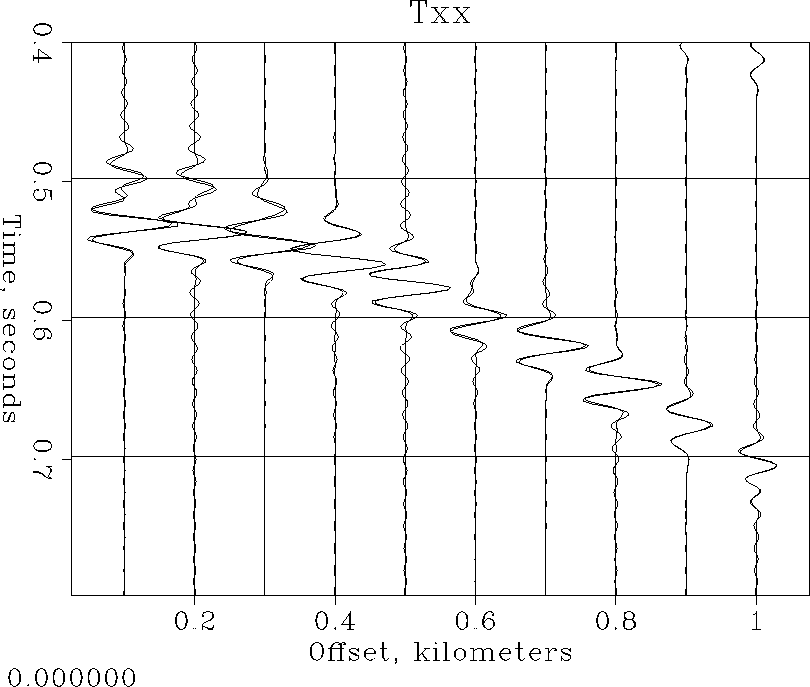
Hopefully you enjoyed this example and you are ready to try more. If you are familiar with UNIX you can build a shell script to do all this automatically so that you don't have to retype it again and again. If you are really ambitious, create a shell script that lets you specify the power of two to subsample by. Figure  shows what happens if you subsample by a factor of four and reinterpolate back using our Fourier-domain method. (This time we subsampled too far and our sinc functions got out of control!)

 

Fourier
Figure 6 Wiggle overplot=y par=plotpar poly=n | Pspen

Different people use SEPlib programs different ways. Some prefer to type everything themselves as we have been doing here. Some write everything as shell scripts. Others like to do everything from within Makefiles (or Cakefiles). How you use SEPlib is up to you.