Gassmann Saturated Velocity Predictions

In this section, we calculate saturated velocities for Massillon Sandstone using the dry sandstone measurements and Gassmann's Equation. Gassmann's Equation relates dry elastic moduli to fluid-saturated elastic moduli. For compressional moduli, Gassmann can be stated as follows:

where M is a normalized ratio of mineral, fluid and dry bulk moduli such that

as rearranged from Equation 2.77 of Bourbié et al. (1987). Concerning shear moduli, Gassmann makes no distinction between dry and saturated properties:

In the above expressions, K_m is the ¶ modulus of the pure mineral skeleton, K_f is the ¶ modulus of the saturating fluid, and K_d is the ¶ modulus of the dry rock under study. K_s is the Gassmann theoretical ¶ modulus of the dry rock after complete saturation with wetting fluid. Similarly, is the Gassmann theoretical shear modulus predicted to be the same as the dry bulk shear modulus $\mu_d$.The underlying assumptions in Gassmann's Equation are: (1) the rock satisfies linear isotropic elasticity, (2) the rock skeleton is comprised of one single homogeneous mineral phase, (3) the wetting fluid is homogeneous and completely saturates the porosity, (4) the porosity is uniform throughout the sample, and (5) the measurements are made at low (asymptotically zero) frequency.

To evaluate K_s, values for K_m, K_f, K_d, and are required. The K values can be obtained through the generic relation

Using the given dry bulk density = 2030 kg/m³, and the measurement = 2918 m/s, the dry ¶ modulus can be calculated to be K_d = 9.2 GPa. Water was used as the wetting fluid, which has a velocity of = 1500 m/s, a density of = 1000 kg/m³, and hence a ¶ modulus of K_f = 2.25 GPa. The dry bulk density can be expressed as . Using a porosity of = 0.221 gives a solid mineral density of = 2606 kg/m³. This value compares well with tabulated values of 2650 kg/m³ for quartz, if one also accounts for a finite component of less dense feldspar in the sandstone. For the ``pure'' mineral bulk modulus, we calculated the Voigt average to be = 11.8 GPa. This value is probably truly an average of the quartz, clay and feldspar content in Massillon Sandstone, as it does not compare well with tabulated solid quartz values of K_q = 38 GPa. Substituting these values into Gassmann's relation gives a saturated ¶ modulus of K_s = 9.7 GPa. The § modulus can be obtained as = 6.1 GPa. The saturated density is = 2251 kg/m³. Finally, the saturated ¶ and § velocities estimated by Gassmann are:

and

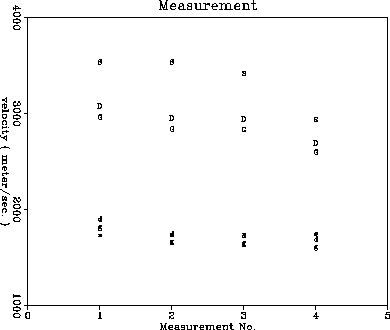
The final Massillon sandstone velocity results for each of our four independent experiments are plotted in Figure . The median data set from Experiment 3 has been the focus of our current and upcoming discussion.

 

Data
Figure 4 Massillon sandstone velocities measured in the lab and predicted by the Gassmann equation; D = P-wave velocity measured for the dry sample, S = P-wave velocity measured for the saturated sample, G = P-wave velocity predicted by the Gassmann equation, d = S-wave velocity measured for the dry sample, s = S-wave velocity measured for the saturated sample, g = S-wave velocity predicted by the Gassmann equation.