USE OF MODEL WEIGHTING FUNCTIONS

While the masked operator method works well for synthetic data it is difficult to apply to real data. The masking operator is an ``all or nothing'' operator, data is classified either as ``aliased'' or ``unaliased.'' It is hard to create a good mask function for real data because of the presence of noise, amplitude variation along events etc. If an incorrect mask function is used the masked operator may become singular or have a large null space. The iterative solution process converges very slowly and it may produce spurious high amplitudes in the $p-\tau$ domain.

A more robust method is one that penalizes energy in the regions identified as ``aliased'' but does not force it to be zero. This method may be slower to converge than the mask method if the mask is chosen correctly but it will not fail completely if the weighting function is chosen poorly.

The new method minimizes the sum of the data mismatch and a weighted length measure.

$$min \vert\vert L\, U(p,\omega)\ -\ U(x,\omega) \vert\vert^2 + \vert\vert W\, U(p,\omega) \vert\vert^2.$$

The weighting operator is a diagonal operator with weights that are high where the data is assumed to be aliased and low where it is assumed to be unaliased. If this problem is interpreted as a maximum likelihood scheme the operator W is an estimate of the inverse model covariance matrix. The diagonal operator implies that model parameters are uncorrelated, with a variance that is low (where W is high) in the areas where the prior model (zero) is expected to be a good estimate, and high where the data is likely to be different from zero.

The new problem can be solved by casting it in the form of the linear system of equations,

$$\pmatrix { A \cr W }\, U(p,\omega) = \pmatrix{ U(x,\omega) \cr 0 }$$

This system of equations is again solved using a simple conjugate gradient method.

I generate the weighting function in a manner similar to the masking function. Instead of using a threshold to convert the continuity function into a zero or one I scale the values to lie in the range zero to one. The inverse of this value is used as the weighting factor in calculating the weighted length of the model vector.

Figure  shows the inverse weighting function derived from the three-dip synthetic data and figure  shows the result of the inversion. As expected a little aliased energy has leaked through. This could be avoided by using a more severe weighting operator.

 

three-weightop Figure 12 Inverse weighting operator displayed in the 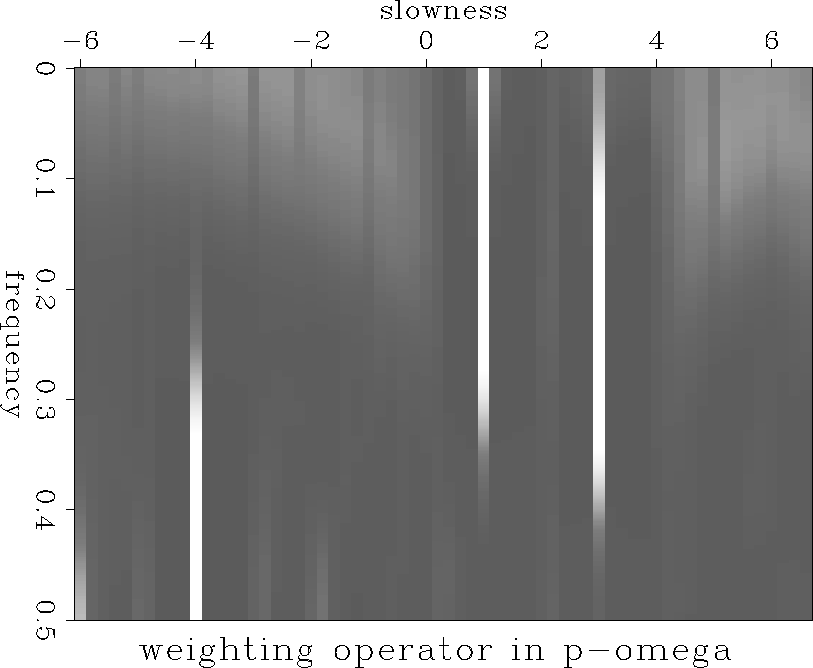$p-\omega$ domain, the maximum value is 1.0

 

three-weightlsq Figure 13 $p-\omega$ spectrum of the least squares inverse slant stack using the weighted operator.