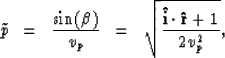|
reflect
Figure 10 The points where the ascending and descending wavefronts overlap define the location of the reflector. The reflection angle can be determined by the gradients of the two wavefields at the reflection point, at the time when the reflection occurred. |  |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a descending (incident) wavefield crossing
an ascending (reflected) wavefield at a given time step of the
backward propagation part of the scheme. The crossing point defines
the point of the interface that was imaged at that time, and the
angles
shows a descending (incident) wavefield crossing
an ascending (reflected) wavefield at a given time step of the
backward propagation part of the scheme. The crossing point defines
the point of the interface that was imaged at that time, and the
angles