Next: IMPLEMENTATION ON THE CONNECTION
Up: Popovici : PSPI and
Previous: THE PHASE SHIFT PLUS
Stoffa et al. (1990) present an alternative to the PSPI, replacing the
downward continuation step with two or more velocities by a single
average velocity followed by a phase shift of the wavefield with a
perturbation term to account for lateral velocity variations.
The Split-step algorithm is based on splitting the space variant
slowness (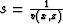 ) into a constant term and a perturbation
term,
) into a constant term and a perturbation
term,
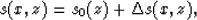
where s0(z) is a reference slowness defined as the average slowness
in a depth interval.
The wave equation (1) is Fourier transformed along the time
axis to become
| 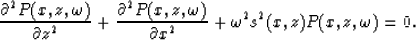 |
(7) |
After inserting the slowness split into the perturbation term and
the average term the equation is transformed into
| ![\begin{displaymath}
{\partial^2 P(x,z,\omega) \over \partial z^2}+
{\partial^2 P...
...omega^2[2 s_0(z) \Delta s(x,z)+\Delta s^2(x,z)] P(x,z,\omega) .\end{displaymath}](img20.gif) |
(8) |
Noting the right side of the equation
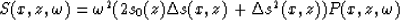
equation (8) becomes
| 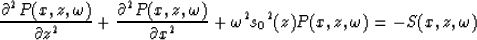 |
(9) |
which is an inhomogeneous wave equation with a source
term 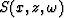 .
.
Stoffa et al. show that
equation (9) can be integrated over a thin depth layer 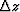 by ignoring the contribution of the
by ignoring the contribution of the 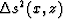 .Equation (9) is Fourier transformed in surface coordinates
after the second
order term of the slowness perturbation is dropped and subsequently
integrated over the depth layer
.Equation (9) is Fourier transformed in surface coordinates
after the second
order term of the slowness perturbation is dropped and subsequently
integrated over the depth layer 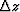 .
After inverse Fourier transformation back into surface coordinates the solution
has the form
.
After inverse Fourier transformation back into surface coordinates the solution
has the form
| 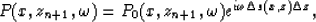 |
(10) |
where 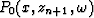 represents the wavefield downward continued
with the average slowness s0(z).
Though the mathematical path is very different from the one Gazdag (1984)
followed, the solution is very similar if you consider Gazdag's algorithm
with a single velocity.
represents the wavefield downward continued
with the average slowness s0(z).
Though the mathematical path is very different from the one Gazdag (1984)
followed, the solution is very similar if you consider Gazdag's algorithm
with a single velocity.
The phase subtraction and addition trick in Gazdag's algorithm is replaced
by multiplication with
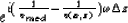
after the downward extrapolation.
Compared with Gazdag's trick to phase shift with
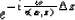
followed by
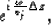
the only difference is that Gazdag (1984) does the first phase shift
before the Fourier transform while Stoffa et al. (1990) do it after
the Fourier transform. Though analytically not identical in the
general case, the qualitative idea is the same.
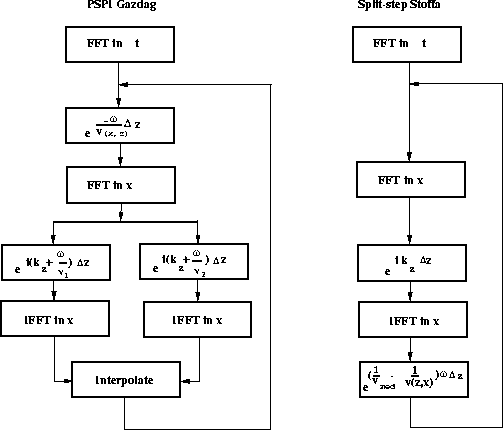
The two algorithms are compared in Figure 1.
gazsplit
Figure 1 The two Fourier
migration algorithms. a) Phase Shift Plus Interpolation (PSPI).
b) Split-step Fourier Migration.






Next: IMPLEMENTATION ON THE CONNECTION
Up: Popovici : PSPI and
Previous: THE PHASE SHIFT PLUS
Stanford Exploration Project
12/18/1997
![]() ) into a constant term and a perturbation
term,
) into a constant term and a perturbation
term,
![]()
![]()
![]() by ignoring the contribution of the
by ignoring the contribution of the ![]() .Equation (9) is Fourier transformed in surface coordinates
after the second
order term of the slowness perturbation is dropped and subsequently
integrated over the depth layer
.Equation (9) is Fourier transformed in surface coordinates
after the second
order term of the slowness perturbation is dropped and subsequently
integrated over the depth layer ![]() .
After inverse Fourier transformation back into surface coordinates the solution
has the form
.
After inverse Fourier transformation back into surface coordinates the solution
has the form
![]()
![]()
![]()