THE COURANT-FRIEDRICHS-LEWY CONDITION

The Courant-Friedrichs-Lewy (CFL) condition states that a necessary condition for the convergence of an explicit finite difference scheme is that the domain of dependence of the discrete problem includes the domain of dependence of the differential equation in the limit as the length of the finite difference steps goes to zero.

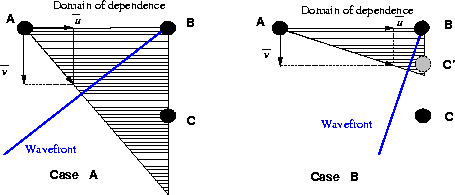
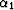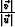The CFL condition is easy to understand when examining the two cases in Figure 1. In the first case, the plane wave propagates with an angle ${\alpha}_1$ given by the arctangent of the two vectors ${\vert\vec{v}\vert} \over {\vert\vec{u}\vert}$.The explicit upwind finite difference stencil will use the traveltime values in points A and B to calculate the value in point C. When the plane wave propagates with an angle 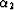${\alpha}_2$ as in the second case, the information from points A and B is propagated to the right and above point C. In this case the point C is outside the domain of dependence and numerical instabilities can appear. To ensure the stability of the algorithm I use an adaptive step algorithm which will calculate the position of the point C' inside the domain of dependence.

 

stencil
Figure 1 Two cases in plane wave propagation for the explicit finite difference traveltime algorithm. a) The domain of dependence includes the new stencil point. b) The domain of dependence doesn't include the stencil point C, requiring an adaptive step at C'.