Interlacing

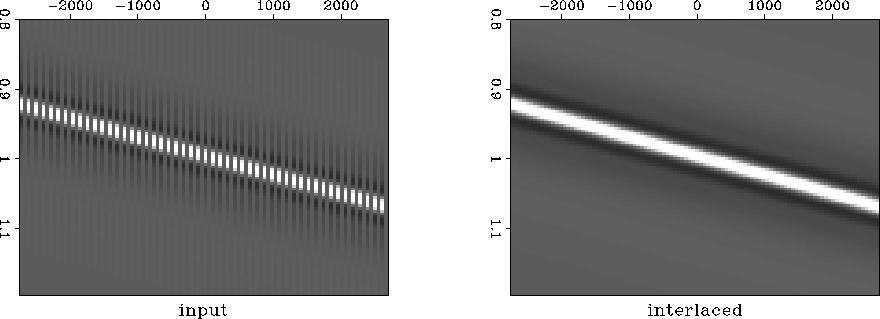
Interlacing a data set is equivalent to shifting to new location by 1/2 a gridpoint. This assumes a regular starting geometry. Figure fills in missing data at every other grid point by actually projecting the model space p-$\tau$ onto a data geometry with twice as many traces. Much more common than this data interlacing problem, is the need for filling gaps in the data, due to trace editing or irregular acquisition. Figure showed an example of an acquisition gap and its reconstruction. Figure fills in missing traces by estimating the p-$\tau$ domain in a least squares sense for the given geometry and then projecting the model back onto the new geometry.

 

interlace
Figure 3 The p-$\tau$ domain is estimated in a least squares sense for the given geometry. The best fitting model is projected back onto the new geometry (missing trace construction).