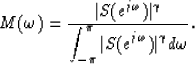Next: APPLICATIONS
Up: THEORY
Previous: Factorizing for minimum phase
Another way to overcome the problem of phase-wrap-around is to
compute the phase spectrum by integrating its derivative. The phase
spectrum of a signal is related to its Fourier transform as follows:
| ![\begin{displaymath}
\Phi_s(\omega) = \Im[\ln S(\omega)].\end{displaymath}](img19.gif) |
(8) |
Taking the derivative with respect to 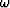 on both sides gives
on both sides gives
| ![\begin{displaymath}
{d\Phi(\omega) \over d\omega} = \Im[{S^\prime(\omega) \over S(\omega)}].\end{displaymath}](img21.gif) |
(9) |
If we assume 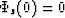 , then
, then
| 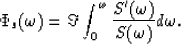 |
(10) |
The phase spectrum computed in this way is continuous. Furthermore,
it can be shown (Oppenheim and Schafer, 1975) that
| 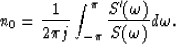 |
(11) |
If we define the group delay as
| 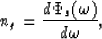 |
(12) |
then equation (11) tells us that n0 is an average group delay
over frequency range ![$[-\pi,\pi]$](img26.gif) .Considering the limited band width of the seismic signals and the presence of
noises, we should include uneven weights in the averaging step of
equation (11) as follows:
.Considering the limited band width of the seismic signals and the presence of
noises, we should include uneven weights in the averaging step of
equation (11) as follows:
| 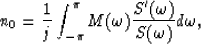 |
(13) |
where 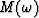 is a weighting function. One choice of the weighting
function is
is a weighting function. One choice of the weighting
function is
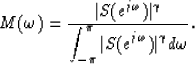
If 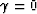 , the result is the evenly weighted average of the group delay.
If
, the result is the evenly weighted average of the group delay.
If 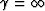 , the result is equal to the group delay of the frequency
corresponding to the peak amplitude spectrum.
, the result is equal to the group delay of the frequency
corresponding to the peak amplitude spectrum.





Next: APPLICATIONS
Up: THEORY
Previous: Factorizing for minimum phase
Stanford Exploration Project
12/18/1997