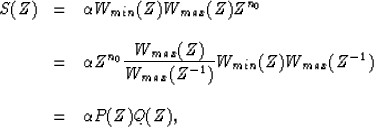
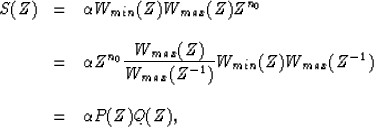 |
(7) |
![]()
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows an
example with the same field data as in Figure
shows an
example with the same field data as in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . We see
that two factors of this factorization process have similar frequency
content. As expected, the traveltimes picked by two methods are equal.
Because the phase spectrum of an allpass filter is always a nondecreasing
function, the procedure for unwrapping the phase of P(Z) is easier than that
for S(Z).
. We see
that two factors of this factorization process have similar frequency
content. As expected, the traveltimes picked by two methods are equal.
Because the phase spectrum of an allpass filter is always a nondecreasing
function, the procedure for unwrapping the phase of P(Z) is easier than that
for S(Z).
|
vwkfact
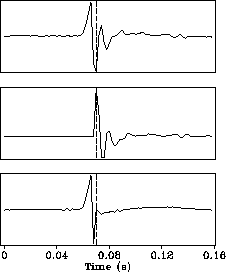
Figure 4 The top panel shows the same trace as one in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The middle and bottom panel show the minimum phase and allpass parts of this
wavelet, respectively. The vertical dashed lines indicate
the picking positions.
The fat, dashed curve superposed on the curve of the top panel is the
signal reconstructed from two factorized parts. .
The middle and bottom panel show the minimum phase and allpass parts of this
wavelet, respectively. The vertical dashed lines indicate
the picking positions.
The fat, dashed curve superposed on the curve of the top panel is the
signal reconstructed from two factorized parts.
|  |