LOCAL WAVEFRONT EXTRAPOLATION

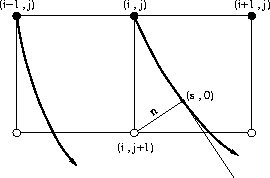As in the case of the finite difference method, the description of the computational scheme of the local paraxial ray method consists of two parts. The first part addresses the local computation that determines how the traveltime and amplitude at a point are computed from the traveltimes and amplitudes at its neighbors. The second part explains the order in which the local computation proceeds. This note focuses on the description of the principles of the local computation. It should not be difficult to adapt these principles to the propagation schemes developed by Vidale and others.

 

loray Figure 2 Local paraxial wavefront extrapolation.

The local computational scheme of the local paraxial ray method can be divided into two steps. As shown in Figure , we assume that we know the traveltimes, the ray directions, the second-order partial derivatives of the traveltimes with respect to n, and the values of the Jacobian function at the grid points marked with dots, and we want to compute these quantities at the grid points marked with circles. The first step is to trace rays locally from every grid point marked with a dot and to compute traveltime $\tau(s,0)$, function M(s,0), and Jacobian J(s,0) along each ray. To do so, we need to solve the ray equation and equation (3), and perform the integrations in equations (1) and (2). The second step interpolates these quantities computed along the rays onto the grid points marked with circles. Let us take grid point (i,j+1) as an example. As indicated in Figure , we can find ray-centered coordinates (s,n) of this point that are associated with the ray traced from grid point (i,j). If we assume that the grid sizes are small enough that the paraxial approximation is always valid, then we can use equation (4) to find the traveltime at grid point (i,j+1) and use equation (7) to compute the value of the Jacobian function that is related to the amplitude at this point. Two other quantities are required in order to continue the local ray tracing from the grid point (i,j+1). One is the ray direction at this point. The ray direction can be determined from the gradient of the traveltime that can be computed from equation (5). The other quantity is the value of function M(s,n), which serves as the initial condition of the dynamic ray tracing equation at this point and can be computed from equation (6). If possible, we do the same computation for each ray passing by point (i,j+1) and pick the result that is associated with the minimum traveltime. This completes the local computation.