




Next: RELATION TO CLAERBOUT'S AND
Up: Ji: Trace Interpolation
Previous: SPECTRAL ESTIMATION
The interpolation considered in this paper is first-order interpolation,
achieved by interlacing the space axis.
Higher-order interpolation can be obtained by applying the
first-order interpolation scheme several times.
Now we know the spectrum which is supposed to result after interpolation,
our next step is to find a filter which has an amplitude spectrum that
is inverse to the spectrum we estimate.
The filter can be found in both the t-x domain and the f-x domain.
In this paper, I choose the f-x domain for its simplicity.
The procedure for an interpolation can be summarized as follows:
- 1.
- I pad zeros in the time domain with the same number of original
time samples, and Fourier transform over time to
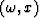 .
. - 2.
- For each frequency from zero to half Nyquist, I find
a minimum phase wavelet whose inverse spectrum is the spectrum of
the signal along the x axis. Here, I used Kolmogoroff spectral
factorization for finding minimum phase filters.
- 3.
- For each frequency, I find missing data by minimizing the
filtered output in the least-squares sense using a conjugate-gradient algorithm.
The filter applied is the wavelet which comes from the half frequency.
Another approach for finding filters is to obtain a prediction-error filter
for each frequency, because the prediction-error filter has a spectrum that
is inverse to the input (Claerbout, 1991).
If you want to limit the length of filter, the prediction-error filter is
more attractive than spectral factorization.





Next: RELATION TO CLAERBOUT'S AND
Up: Ji: Trace Interpolation
Previous: SPECTRAL ESTIMATION
Stanford Exploration Project
12/18/1997