




Next: MODEL RESULTS
Up: LABORATORY AND NUMERICAL MODELS
Previous: LABORATORY AND NUMERICAL MODELS
Before examining our simplified numerical simulation of Vernik and Nur's
experiment, we will first show two complementary ``ideal''
simulated experiments, one designed for measuring the vertical group velocity
and the other one for measuring the vertical phase velocity.
The lower plot in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows how vertical group velocity could
be properly measured by using extremely small source and receiver transducers.
The anisotropic wavefront radiates out from the point source at the bottom;
the point receiver at the top detects the part of the wavefront with
vertically traveling energy as it passes by.
The distance between the two transducers
divided by the measured traveltime gives the vertical group velocity.
shows how vertical group velocity could
be properly measured by using extremely small source and receiver transducers.
The anisotropic wavefront radiates out from the point source at the bottom;
the point receiver at the top detects the part of the wavefront with
vertically traveling energy as it passes by.
The distance between the two transducers
divided by the measured traveltime gives the vertical group velocity.
The upper plot in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows how true phase velocity could be properly
measured. The source must be wide enough to launch a reasonable facsimile of
a plane wave. Since the source is not infinite, the ``plane wave'' is
truncated; the receiver on the top must be positioned where it can sample
the flat central part of the wavefront, away from the diffracting truncated
edge.
Note that while the source transducer runs from -20 to +20 mm, the
flat part of the wavefront in the figure runs from -30 to +10.
While the wavefront has traveled vertically 40mm from the bottom of
the model to the top, it has also slipped sideways 10mm.
The receiver in the upper plot in Figure
shows how true phase velocity could be properly
measured. The source must be wide enough to launch a reasonable facsimile of
a plane wave. Since the source is not infinite, the ``plane wave'' is
truncated; the receiver on the top must be positioned where it can sample
the flat central part of the wavefront, away from the diffracting truncated
edge.
Note that while the source transducer runs from -20 to +20 mm, the
flat part of the wavefront in the figure runs from -30 to +10.
While the wavefront has traveled vertically 40mm from the bottom of
the model to the top, it has also slipped sideways 10mm.
The receiver in the upper plot in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , while OK, is perilously
close to the edge; a position 10 or 15 millimeters further to the left
would have been better.
Note that if the source transducer had been infinite,
there would be no such complications:
the position of the receiver would be irrelevant.
, while OK, is perilously
close to the edge; a position 10 or 15 millimeters further to the left
would have been better.
Note that if the source transducer had been infinite,
there would be no such complications:
the position of the receiver would be irrelevant.
The upper plot in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) was constructed
by summing multiple copies of the lower plot in Figure
was constructed
by summing multiple copies of the lower plot in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shifted from -20 to +20 mm.
The flat part of the wavefront in the upper plot is the sum of all
the shifted copies of the highest point on the wavefront
in the lower plot. From this basic relationship, we can see that
we could have measured the vertical phase velocity directly
from the lower plot by simply shifting the receiver over
to where the wavefront first encountered the upper surface (around the
-11mm position) and dividing by
the vertical distance from source to receiver (40mm in the figure).
Note this distance is less than the true distance between
the source and the offset receiver (which would be
shifted from -20 to +20 mm.
The flat part of the wavefront in the upper plot is the sum of all
the shifted copies of the highest point on the wavefront
in the lower plot. From this basic relationship, we can see that
we could have measured the vertical phase velocity directly
from the lower plot by simply shifting the receiver over
to where the wavefront first encountered the upper surface (around the
-11mm position) and dividing by
the vertical distance from source to receiver (40mm in the figure).
Note this distance is less than the true distance between
the source and the offset receiver (which would be 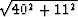 mm).
We are now ready to examine similar figures showing the situation
in Vernik and Nur's experiment.
mm).
We are now ready to examine similar figures showing the situation
in Vernik and Nur's experiment.
phasegroup
Figure 3
Snapshots demonstrating the two ``ideal'' core-sample experiments.
The positions and sizes of the source and receiver transducers are
indicated respectively
by thick horizontal lines at the bottom and top of the model.
Top: an infinite-source experiment for measuring
vertical phase velocity.
Bottom: a point-source to point-receiver experiment
for measuring vertical group velocity.
(As you can see the two experiments are really approximations,
the ``infinite'' transducer is 40mm wide
and the ``point'' transducers are 2mm wide.)
The labeled vertical and near-vertical distances mark the progress of
key points on the radiated wavefront during its travels
from the source up to the top of the model.
Three distinct velocities are indicated:
the vertical group (energy) velocity,
the vertical phase (plane-wave) velocity,
and finally the (nonvertical) group velocity associated with
the vertical phase velocity.
(If the medium were isotropic, all three of these would be equivalent.)






Next: MODEL RESULTS
Up: LABORATORY AND NUMERICAL MODELS
Previous: LABORATORY AND NUMERICAL MODELS
Stanford Exploration Project
12/18/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows how vertical group velocity could
be properly measured by using extremely small source and receiver transducers.
The anisotropic wavefront radiates out from the point source at the bottom;
the point receiver at the top detects the part of the wavefront with
vertically traveling energy as it passes by.
The distance between the two transducers
divided by the measured traveltime gives the vertical group velocity.
shows how vertical group velocity could
be properly measured by using extremely small source and receiver transducers.
The anisotropic wavefront radiates out from the point source at the bottom;
the point receiver at the top detects the part of the wavefront with
vertically traveling energy as it passes by.
The distance between the two transducers
divided by the measured traveltime gives the vertical group velocity.
