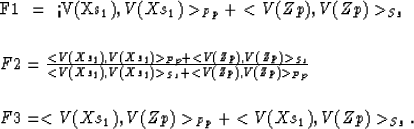Next: SYNTHETIC DATA EXAMPLES
Up: ESTIMATION OF SEPARATION PARAMETERS
Previous: P-S wave separation
One way to calculate the objective function is to take the 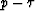 data, apply a separation operator, calculate a set of constant
velocity stacks, and finally calculate the objective function in
velocity stack space. If a repeated calculation of the objective
function is required this would appear to be prohibitively expensive
since each calculation involves a set of constant velocity stacks.
However this cost can be overcome by reordering the operations. The
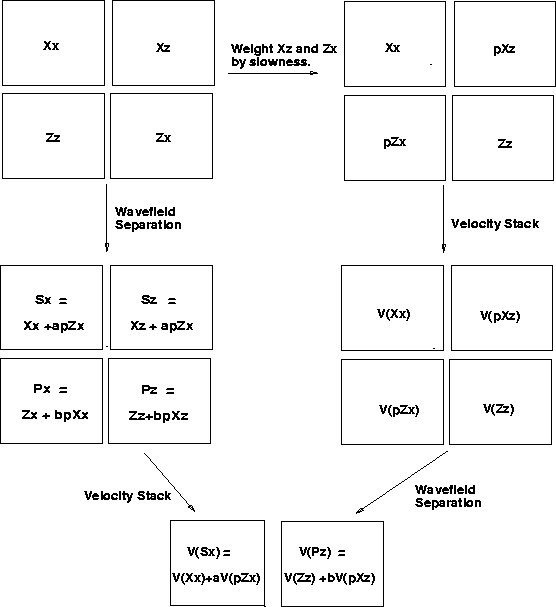
idea is illustrated in figure
data, apply a separation operator, calculate a set of constant
velocity stacks, and finally calculate the objective function in
velocity stack space. If a repeated calculation of the objective
function is required this would appear to be prohibitively expensive
since each calculation involves a set of constant velocity stacks.
However this cost can be overcome by reordering the operations. The
idea is illustrated in figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The wavefield
separation and the velocity stack are both linear operators. These
operators can be reordered so that only one velocity stack step is
necessary. A weighted combination of the velocity stacks can be used
to calculate a velocity stack for the separated data.
. The wavefield
separation and the velocity stack are both linear operators. These
operators can be reordered so that only one velocity stack step is
necessary. A weighted combination of the velocity stacks can be used
to calculate a velocity stack for the separated data.
flowdiag
Figure 3 Equivalent methods of calculating the velocity spectra of data separated with different operators.

The calculation of the objective functions is relatively simple. For
example consider the receiver separation operator for the P-S1
wavetypes. The original data is Xx, Xz, Zx, and Zz data in
the 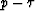 domain. The following velocity panels are calculated,
V(Xx), V(pXz), V(pZx), V(Zz). We can then calculate the
velocity panels for the separated data by taking a linear combination
of these panels.
domain. The following velocity panels are calculated,
V(Xx), V(pXz), V(pZx), V(Zz). We can then calculate the
velocity panels for the separated data by taking a linear combination
of these panels.
I define the cross-energy operators for the Pp and Ss corridors in
velocity spaceas
The three proposed objective functions can then be written as,
On substituting the expressions for the separated velocity panels and minimizing
by setting
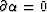 and
and 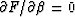 ,
I obtain explicit expressions for
,
I obtain explicit expressions for  and
and 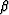 from the F1 and F3 objective functions. The F2 objective function
does not produce such a simple result but a scan of possible parameters is
a relatively cheap operation:
from the F1 and F3 objective functions. The F2 objective function
does not produce such a simple result but a scan of possible parameters is
a relatively cheap operation:
- F1
-
- F3
-





Next: SYNTHETIC DATA EXAMPLES
Up: ESTIMATION OF SEPARATION PARAMETERS
Previous: P-S wave separation
Stanford Exploration Project
12/18/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The wavefield
separation and the velocity stack are both linear operators. These
operators can be reordered so that only one velocity stack step is
necessary. A weighted combination of the velocity stacks can be used
to calculate a velocity stack for the separated data.
. The wavefield
separation and the velocity stack are both linear operators. These
operators can be reordered so that only one velocity stack step is
necessary. A weighted combination of the velocity stacks can be used
to calculate a velocity stack for the separated data.
![\begin{eqnarraystar}
V(Xs_1) & = & V(Xx)\,+\,\alpha\,V(pXz) \\ [.25in] V(Zp) & = &
V(Zz)\,+\,\beta\,V(pZx) \\ \end{eqnarraystar}](img16.gif)
![\begin{eqnarraystar}
<A,B\gt _{Pp} & = & \Sigma_{i,j \in Pp} A(i,j) B(i,j) \\ [.25in]
<A,B\gt _{Ss} & = & \Sigma_{i,j \in Ss} A(i,j) B(i,j) \cr\end{eqnarraystar}](img17.gif)