Next: Testing the method on
Up: Cunha and Claerbout: Multiple
Previous: Introduction
Multiple suppression in the velocity domain can be formulated
as an optimization problem.
The aim is to find some ``model" in the space-time
domain, which, when added to the original CMP gather, minimizes the
power within a pre-specified window in the velocity-time domain.
The precise mathematical formulation follows.
Let 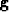 represent the original CMP gather,
represent the original CMP gather, 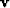 its velocity
transform, and N the velocity transform operator
its velocity
transform, and N the velocity transform operator
| 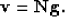 |
(1) |
Then, we want to find the unknown model 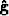 that minimizes
the objective function
that minimizes
the objective function
| 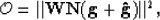 |
(2) |
where 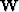 is a windowing operator that selects the region
of the velocity spectrum in which the energy of the multiples
is dominant. To find the solution
is a windowing operator that selects the region
of the velocity spectrum in which the energy of the multiples
is dominant. To find the solution 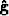 that minimizes
that minimizes 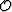 we need to solve
we need to solve
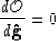
leads to
| 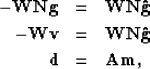 |
(3) |
| |
| |
which is a system of linear equations to be solved for the unknown
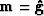 , where the data
, where the data 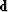 is the windowed velocity
transform of the original data. The system can be over- or under determined,
depending on how the operators
is the windowed velocity
transform of the original data. The system can be over- or under determined,
depending on how the operators 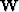 and
and 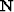 are defined, but it will
usually be large enough, since
are defined, but it will
usually be large enough, since 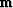 is typically 105 points long. Of
course
is typically 105 points long. Of
course 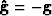 is one of the solutions of
equation 4.
However the window operator
is one of the solutions of
equation 4.
However the window operator 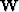 ``transfer" the events that
map outside the window (which are predominantly primaries) to the
null space.
The use of conjugate gradients (CG) seems to be a suitable choice for
solving this problem especially because a few iterations would not only
be enough but would also contribute to the stabilization of the process,
when noise is present.
We have chosen to use a very simple form for the velocity transform
operator
``transfer" the events that
map outside the window (which are predominantly primaries) to the
null space.
The use of conjugate gradients (CG) seems to be a suitable choice for
solving this problem especially because a few iterations would not only
be enough but would also contribute to the stabilization of the process,
when noise is present.
We have chosen to use a very simple form for the velocity transform
operator 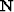 , the nearest neighbor normal moveout-stack. The
advantages of choosing this operator are its computational speed and
the simplicity of its transpose
, the nearest neighbor normal moveout-stack. The
advantages of choosing this operator are its computational speed and
the simplicity of its transpose 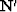 , which is
needed in the conjugate algorithm (Claerbout, 1991).
, which is
needed in the conjugate algorithm (Claerbout, 1991).





Next: Testing the method on
Up: Cunha and Claerbout: Multiple
Previous: Introduction
Stanford Exploration Project
12/18/1997
![]() represent the original CMP gather,
represent the original CMP gather, ![]() its velocity
transform, and N the velocity transform operator
its velocity
transform, and N the velocity transform operator
![]()