The basic idea in Givens rotations is to annihilate a particular off-diagonal element of a matrix (and its symmetric pair). We can zero the elements apq and aqp of matrix A by applying a coordinate rotation given by:
| (1) |
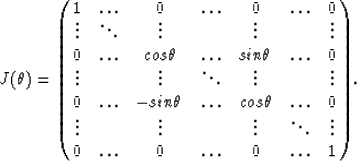
Golub and Van Loan (1989) show that ![]() is given by:
is given by:
| (2) |
| bpp = app - t apq | (3) |
| bqq = app + t apq, | (4) |
| (5) |
On a larger scale, the operation that we perform on the full matrix A is:
| (6) |
 |
(7) |
This method of diagonalizing a matrix is obviously quite expensive in the general case, since there are (n-1)*(n-2)/2 annihilations to perform for an nxn matrix. But in our case, A is very sparse, and we want only to attack the outer diagonals of Table (1), leaving a tridiagonal system that we can solve using traditional methods. The cost should be quite small.
It would be straightforward if this operation zeroed the two off-diagonal
elements and left the rest of the matrix unchanged.
Unfortunately this is not the case. When we pre-multiply
A by ![]() and post-multiply by
and post-multiply by ![]() ,what is modified is not just the two diagonal and two off-diagonal
elements we are interested in, but the whole two rows and two columns
that contain these elements.
,what is modified is not just the two diagonal and two off-diagonal
elements we are interested in, but the whole two rows and two columns
that contain these elements.
In other words, as we move through the matrix, annihilating off-diagonal elements, we create non-zero elements elsewhere, and occasionally fill in previously-created zeros. For this reason, the scheme is not direct but iterative. One pass through the matrix increases the diagonal dominance, but leaves some artifacts. Additional passes gradually knock down these artifacts, and at some point everything off the diagonal is small enough that it can be ignored. Press et al. suggest 6-10 passes are needed for the general case of diagonalizing a matrix. The action of the method is best illustrated by an example, as in the following section.
The method lends itself well to a parallel implementation because a given rotation modifies only two rows or two columns of the matrix. If only one column or row were to be modified in each rotation, we would need only two passes - one for modifying the rows and one for the columns - in order to attack an entire diagonal in parallel. The fact that two rows or columns are modified simultaneously means that four passes (two for rows, two for columns) are required. This is still very few, and suggests that parallel implementations should be extremely fast.