![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
Here is what the code looks like now:
DO IZ=1,NW
A = ACOPY
B = BCOPY
C = CCOPY
C Compute right-hand side
CD = RA*CSHIFT(CMCQ,1,-1) + RB*CMCQ + RC*CSHIFT(CMCQ,1,1)
C Tridiagonal solver
CALL GEN_TRIDIAG_SOLVE( CD,A,B,C,ONE,TOL,IER)
C Lens term
CP = CD * SHIFTS
C Imaging
P(:,1) = SUM(REAL(CP), DIM = 2)
P = CSHIFT(P,2,1)
ENDDO
In this section, I describe the modifications that I made, and show the improvement obtained by each. I show the timings at each step for the 128x1024 problem.
First, notice in the original CM code that I re-compute the diagonal matrices for the tridiagonal solver at each depth step. The reason I did this was because the solver overwrites these matrices. A less costly alternative to re-computing is to save a copy of the matrices and restore from this saved copy each time. These copies are the matrices ACOPY, BCOPY, and CCOPY in the new program. Here is the performance after this modification:
| 4|c|NX=128 NW=1024 | |||
| Elapsed Time (sec) | CM Time (sec) | CM Mflops/sec | |
| Compute RHS | 63.9 | 63.9 | 46 |
| Tridiagonal solver | 17.8 | 17.8 | 648 |
| Lens term | 3.27 | 3.27 | 246 |
| Imaging | 42.3 | 42.3 | 6.4 |
| Loop total | 132 | 132 | 117 |
| Program total | 212 | 209 |
The improvement is all in the ``Loop total'', since the computation of the diagonal matrices was not included in any of the parts of the loop timed individually.
The computation of the right-hand side in the old version, using FORALL statements, was not particularly efficient or easy to read. Fortran 90 provides functions CSHIFT and EOSHIFT to shift an array along a particular axis. CSHIFT performs a circular shift (with wraparound) while EOSHIFT does an end-off shift. EOSHIFT is what we want. It gives, in effect, zero-value boundary conditions. After trying it I noticed the following improvement:
| 4|c|NX=128 NW=1024 | |||
| Elapsed Time (sec) | CM Time (sec) | CM Mflops/sec | |
| Compute RHS | 32.1 | 32.1 | 92 |
| Tridiagonal solver | 17.8 | 17.8 | 648 |
| Lens term | 3.27 | 3.27 | 246 |
| Imaging | 42.3 | 42.3 | 6.4 |
| Loop total | 101 | 101 | 154 |
| Program total | 180 | 177 |
Then, when Biondo Biondi suggested that CSHIFT is faster than EOSHIFT in the current CM compiler, I used it instead and noticed an even larger improvement:
| 4|c|NX=128 NW=1024 | |||
| Elapsed Time (sec) | CM Time (sec) | CM Mflops/sec | |
| Compute RHS | 10.8 | 10.8 | 274 |
| Tridiagonal solver | 17.8 | 17.8 | 648 |
| Lens term | 3.27 | 3.27 | 246 |
| Imaging | 42.2 | 42.2 | 6.4 |
| Loop total | 79.3 | 79.3 | 196 |
| Program total | 158 | 156 |
Using CSHIFT gives circular boundary conditions. But I eliminated the unwanted wraparound in the shift by placing zeroes at the ends of the RA and RC right-hand side tridiagonal coefficient matrices, so the effect is the same as using EOSHIFT.
It may be that this code is still not optimal. Generally speaking EOSHIFT and CSHIFT operations should be used only on parallel axes. When used in the serial direction, as they are here, they may not be as efficient as a plain Fortran loop. For the problems tried thus far, however, I have found this method to be the fastest.
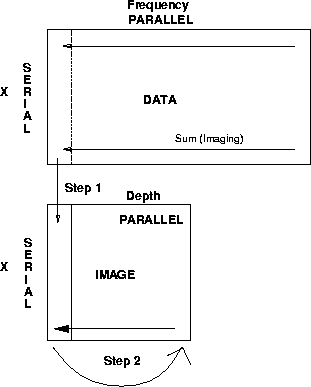
Finally the speed of imaging was improved by two
more modifications suggested by Biondo. First,
I had the imaging step always sum into the z=1 level of
the output image rather than summing into the correct place.
The fact that the destination of the sum is a constant location
helps the compiler to optimize inter-processor communication.
I then perform a CSHIFT to cycle the depth levels around
to make sure that the z=1 level is free for the next
imaging step. This operation is summarized in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
 |
Along with this modification, I changed the size of one of the axes of the output image from the number of depths to the number of frequencies. This change forces the compiler to align the output image with the other arrays whose size depends on the number of frequencies (most of the arrays in the program). The resulting performance:
| 4|c|NX=128 NW=1024 | |||
| Elapsed Time (sec) | CM Time (sec) | CM Mflops/sec | |
| Compute RHS | 10.8 | 10.8 | 274 |
| Tridiagonal solver | 17.8 | 17.8 | 648 |
| Lens term | 3.28 | 3.28 | 246 |
| Imaging | 13.0 | 13.0 | 21 |
| Loop total | 50 | 50 | 311 |
| Program total | 129 | 127 |
The code is now running at more than 300 Mflops/sec, and is roughly 25 times faster than a well-vectorized Convex version. The imaging step is by far the slowest, and accounts for more than one fourth of the time spent in the depth loop.
With these fixes, there is now essentially no difference, for large problems, between the speed of the (:SERIAL,:NEWS) version discussed here and a (:NEWS,:NEWS) version where the axes are weighted to favor communication along the x axis (with a weighting factor of five). With this weight, the (:NEWS,:NEWS) achieves the same 311 Mflops/sec on the 1024x128 problem. On the 256x256 problem (as well as smaller problems) it is slightly faster. It runs at 158 Mflops/sec for the 256x256 problem, compared to 136 Mflops/sec for the (:SERIAL,:NEWS) version. On the smallest problem studied here, 64x64, the (:NEWS,:NEWS) version runs at 52 Mflops/sec, compared with 33 Mflops/sec for the (:SERIAL,:NEWS) program.
It may seem puzzling at first that the performance is poorer for smaller problems when using a (:NEWS,:NEWS) scheme. For a 64x64 problem, the product of NX and NW is 4096, far more than the number of available processors. Surely all the processors are being used, unlike with a (:SERIAL,:NEWS) ordering, where only 64 processors would be used. If so, why then are the speeds so similar? The answer is that even though all processors are being used in the (:NEWS,:NEWS) case, much time is being spent on inter-processor communication. In the 256x256 case, since there are 128 floating point processors, each one of these will contains 512 data points. Because of the axis weighting, these will likely be adjacent points in x for some particular frequency. The effect is much like a (:SERIAL,:NEWS) ordering, so the performance is similar. With a 64x64 problem, there are only 32 points per physical processor. The smaller problem is ``spread out'' over all the processors. This means that, compared to the larger problem, a greater fraction of the time is spent on inter-processor communication. Thus the resulting speed is slower, as is the speed we would get if we packed all the points into fewer processors in a (:SERIAL,:NEWS) ordering. For small problems, you just can't win.
My conclusion is that for this problem, a (:NEWS,:NEWS) specification with the proper weight on the x axis is the best general layout. It performs as well as a (:SERIAL,:NEWS) ordering for large problems, and slightly better for smaller problems.
My emphasis on the problem with 1024 frequencies and only
128 points in x may seem inappropriate. I would guess that
a typical migration has as many or more points in x than ![]() .My reasons for choosing it had to do with memory limitations
I have experienced on the CM, some of which are still mysterious.
I have found myself limited to a total problem size of no more than 1024x128
or 128K points (though in theory the current program should have
room for around 1024x1024 points on our CM).
Within this limitation, the best speeds are obtained
if we have more points along the frequency axis, since it entails
less inter-processor communication. I believe that, given enough
memory, speeds such as what I reported should be obtainable for
1024 frequencies and x axes in excess of 1024 points.
The key is just the available memory. So I chose a somewhat
skewed example in order to report what I think are speeds
that can realistically be obtained on more reasonably sized
problems, if only the memory is there.
.My reasons for choosing it had to do with memory limitations
I have experienced on the CM, some of which are still mysterious.
I have found myself limited to a total problem size of no more than 1024x128
or 128K points (though in theory the current program should have
room for around 1024x1024 points on our CM).
Within this limitation, the best speeds are obtained
if we have more points along the frequency axis, since it entails
less inter-processor communication. I believe that, given enough
memory, speeds such as what I reported should be obtainable for
1024 frequencies and x axes in excess of 1024 points.
The key is just the available memory. So I chose a somewhat
skewed example in order to report what I think are speeds
that can realistically be obtained on more reasonably sized
problems, if only the memory is there.