




Next: 2-D inversion
Up: SYNTHETIC EXAMPLES
Previous: SYNTHETIC EXAMPLES
In this section, we will apply the previous technique to the
inversion of traveltimes for a cross-well geometry. Synthetic data
were generated through the 1-D isotropic model shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
using
a geometry of 17 sources and 17 receivers equally spaced at the
source and receiver well respectively.
If we plot the components of the slowness vector
,
using
a geometry of 17 sources and 17 receivers equally spaced at the
source and receiver well respectively.
If we plot the components of the slowness vector 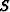 (equation(4)) for
this model, we obtain the profile shown at the right hand side of
Figure
(equation(4)) for
this model, we obtain the profile shown at the right hand side of
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Both slowness components are identical because the model is isotropic.
In this
example, the slowness contrast between the background and the
anomalous layer is small (
.
Both slowness components are identical because the model is isotropic.
In this
example, the slowness contrast between the background and the
anomalous layer is small (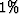 ) and therefore, the propagation
of the energy can be safely modeled by straight ray paths.
) and therefore, the propagation
of the energy can be safely modeled by straight ray paths.
syn-model
Figure 3 Synthetic isotropic model used to test the algorithm.
At the right,
it is shown the slowness vector S that describes this model.
1d-synthetic
Figure 4 Result of the inversion of the synthetic data generated
through the model shown in Figure 3.
|
|  |

We can constrain the
inversion by allowing only vertical variations in the model if it is
know a priori that the medium is layered.
Doing this we eliminate instabilities and non-uniqueness in the inversion
associated with lateral variations, remaining
only those associated with the vertical component of the slowness,
which is not sampled propperly by the recording geometry.
The image area was divided into 100 layers of equal thickness
(8 ft). The inversion process has to estimate
200 parameters from 289 traveltimes. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the slowness vector
obtained after 60 conjugate gradients (CG) iterations.
There is no difference
between the given S (Figure
shows the slowness vector
obtained after 60 conjugate gradients (CG) iterations.
There is no difference
between the given S (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and the estimated one
(Figure
) and the estimated one
(Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
Note also that the results can be represented as a function of depth as well as
a function of the index of the slowness vector.
In the two next results the depth axis will be omitted.
).
Note also that the results can be represented as a function of depth as well as
a function of the index of the slowness vector.
In the two next results the depth axis will be omitted.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the convergence toward the result as a function of the
CG-iterations. The result shown
in Figure
shows the convergence toward the result as a function of the
CG-iterations. The result shown
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) correspond in Figure
correspond in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) to 60 CG-iterations in the axis
number
of iterations. The two ``hills'' represent the slowness at the anomalous layer.
We say that convergence has been achieved when the top and the bottom
of the hills are flat.
Note that
the horizontal component of the slowness converges faster
than the vertical component. This is because in the given model, the
horizontal component of the slowness in the anomalous layer
is better sampled than the vertical component: the range of ray angles
(absolute values)
is from to 53 degrees (
to 60 CG-iterations in the axis
number
of iterations. The two ``hills'' represent the slowness at the anomalous layer.
We say that convergence has been achieved when the top and the bottom
of the hills are flat.
Note that
the horizontal component of the slowness converges faster
than the vertical component. This is because in the given model, the
horizontal component of the slowness in the anomalous layer
is better sampled than the vertical component: the range of ray angles
(absolute values)
is from to 53 degrees (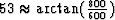 )which is a typical range for cross-well experiments.
)which is a typical range for cross-well experiments.
cg-600x800
Figure 5 Variations of the slowness vector as a function of
the number of conjugate gradient iterations. The original model is
shown at the top.
If the same geometry is used to
generate synthetic data through the model shown at
the top of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (were the well to well separation has been decreased),
we obtain that both components converge at the same rate.
This is because
the vertical component of the slowness is better sampled than before: the
range of ray angles varies between and 76 degrees
(
(were the well to well separation has been decreased),
we obtain that both components converge at the same rate.
This is because
the vertical component of the slowness is better sampled than before: the
range of ray angles varies between and 76 degrees
(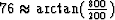 ).
).
cg-200x800
Figure 6 Variations of the slowness vector as a function of
the number of conjugate gradient iterations. The only difference between
the model
shown at the top and the model of Figure 3 is in the horizontal
dimension.
The previous results tell us that
if it is not possible to perform ``enough'' iterations
in order to reach the flat top of both hills (
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
we may wrongly conclude that the medium is anisotropic. What is
really happening is that
the components of the slowness vector do
not converge at the same rate. Severe limited view problems as well as
low signal to noise ratio are some reasons that may limit
the amount of CG-iterations that can be performed before
the ill-conditioning of the problem starts playing any role.
),
we may wrongly conclude that the medium is anisotropic. What is
really happening is that
the components of the slowness vector do
not converge at the same rate. Severe limited view problems as well as
low signal to noise ratio are some reasons that may limit
the amount of CG-iterations that can be performed before
the ill-conditioning of the problem starts playing any role.





Next: 2-D inversion
Up: SYNTHETIC EXAMPLES
Previous: SYNTHETIC EXAMPLES
Stanford Exploration Project
12/18/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
using
a geometry of 17 sources and 17 receivers equally spaced at the
source and receiver well respectively.
If we plot the components of the slowness vector
,
using
a geometry of 17 sources and 17 receivers equally spaced at the
source and receiver well respectively.
If we plot the components of the slowness vector ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Both slowness components are identical because the model is isotropic.
In this
example, the slowness contrast between the background and the
anomalous layer is small (
.
Both slowness components are identical because the model is isotropic.
In this
example, the slowness contrast between the background and the
anomalous layer is small (


