




Next: Absorbing boundary conditions for
Up: Introduction
Previous: Introduction
The 3-D cone dispersion relation of the two-dimensional
scalar wave equation is:
| 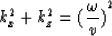 |
(1) |
where kx and kz are the horizontal and vertical wave-numbers,
respectively, and 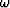 is the temporal frequency. Decomposition of the
wavefield into leftgoing (-x) and rightgoing (+x) waves, requires equation (1)
to be changed into the following form:
is the temporal frequency. Decomposition of the
wavefield into leftgoing (-x) and rightgoing (+x) waves, requires equation (1)
to be changed into the following form:
| 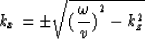 |
(2) |
where the positive sign is used for rightgoing, the negative sign for
leftgoing waves.
Our starting point is that the total wavefield PT at the boundary is
the sum of the incident wavefield PI from the interior and the reflected
wavefield PR from the boundary, such that PT=PI+PR.
If we let PT=PI,
then PR=0, we obtain a perfect nonreflecting boundary. So we use the
leftgoing (rightgoing) wave equation as a boundary condition for the left(right)
edge. To get difference equations in the space-time domain, we need
to rationally approximate equation (2).
Here we give two forms of rational approximation to (2):
| 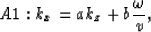 |
(3) |
and
| 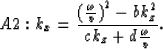 |
(4) |
In the space-time domain:
| 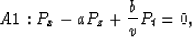 |
(5) |
and
| 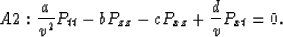 |
(6) |
The criterion for the absorbing boundary condition is that it
is transparent to the incidence wavefield,
that is, the
boundary reflection coefficient is very small.
Our motivation is to find a boundary condition
with a reflection coefficient
as small as possible.
Consider a rightgoing plane wave:
| 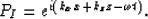 |
(7) |
Suppose the boundary reflection coefficient is R, then the right boundary
reflection is:
| 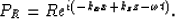 |
(8) |
Locally near the boundary, the total wave field PT=PI+PR must
satisfy both the boundary condition and the interior wave equation.
Applying A2 to (PI+PR), we obtain:
| 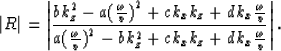 |
(9) |
From the interior two-way wave equation dispersion relation, we have:
| 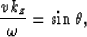 |
(10) |
and
| 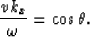 |
(11) |
where 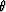 is the angle of incidence measured from the normal to the
boundary. Then we have:
is the angle of incidence measured from the normal to the
boundary. Then we have:
| 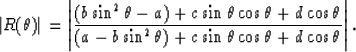 |
(12) |
In the same way we obtain the reflection coefficient for A1:
| 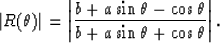 |
(13) |
We first give a reflection coefficient R0=0.1, then by trial and error,
we will find
a, b, c, and d, so that 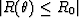 for as many
for as many 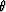 as possible. We have
as possible. We have
A1: a=-0.55, b=1
A2: a=8, b=8, c=-7.5, d=10.
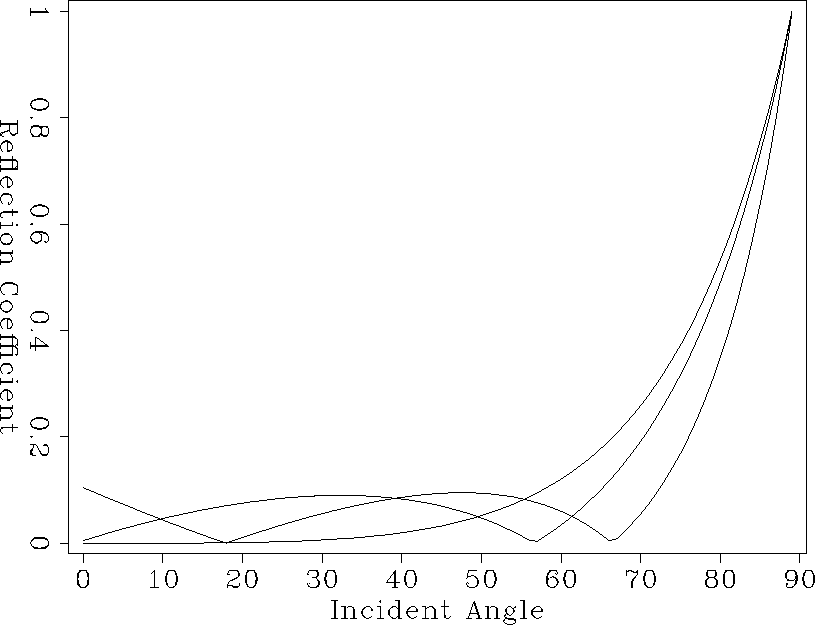
In Figure 1, the reflection coefficients for A1, A2, versus C2 from
Clayton et al. (1977) are plotted. The low angle reflection coefficients
for A1 and A2 can be decreased, but we have to sacrifice the high
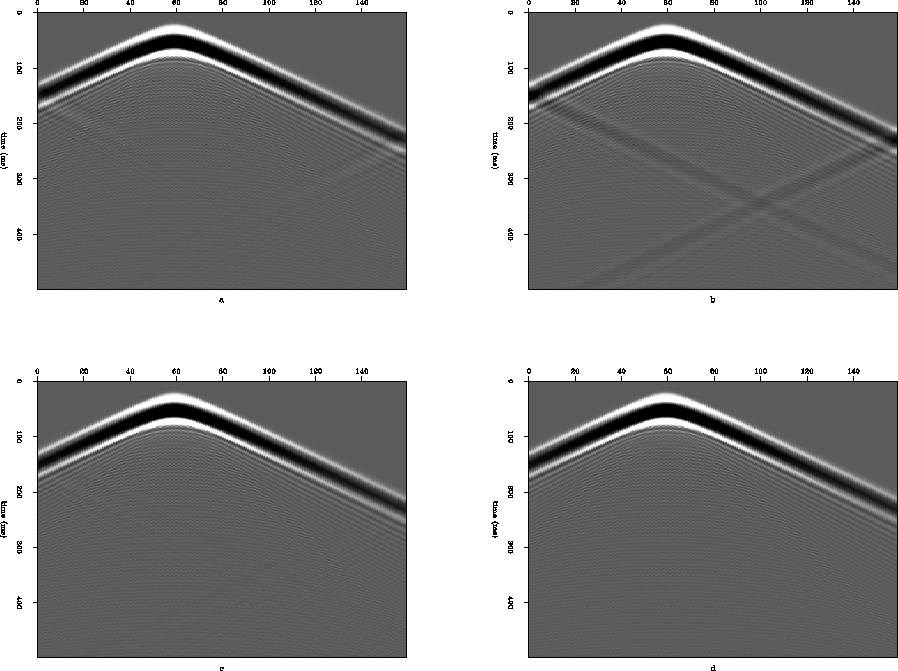
angle counterparts. Figure 2 displays the finite difference modeled
shot records of different absorbing boundary conditions on the model
given by Reynolds (1978, p. 1103).
fig1
Figure 1
Graph of reflection coefficients for boundary conditions,
A1, A2 versus C2 (Clayton et al. 1977).





fig2
Figure 2
Modeled shot records by different absorbing boundary conditions,
(a) A1, (b) A2, (c) C2 by Clayton et al. (1977), (d) Reynolds (1978)










Next: Absorbing boundary conditions for
Up: Introduction
Previous: Introduction
Stanford Exploration Project
12/18/1997
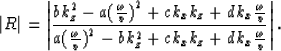
![]() for as many
for as many ![]() as possible. We have
as possible. We have
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()