




Next: About this document ...
Up: Popovici : MZO
Previous: References
The proposition I want to prove is that the vector perpendicular to the
constant-offset isochron bisects the angle between the ray coming
from the source and the one returning to the receiver.
This is the direction of the zero-offset ray, as the incident angle is equal to
the reflected angle and the zero-offset ray bisects both angles.
The gradient to a constant-offset isochron is a vector
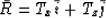
where
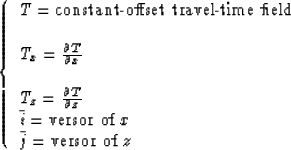
The constant-offset travel-time field can be decomposed into the sum of
the travel-time from the source (Ts) and the travel-time to the receiver
(Tr).
The vector 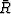 can be therefore as the sum of vectors
can be therefore as the sum of vectors
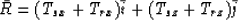
where Tsx, Tsz, Trx, Trz are the partial derivatives of the
travel-time from source and receiver, respectively.
If we note
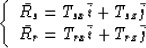
then
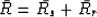
which are two vectors: 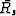 along the ray from the source and
along the ray from the source and
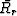 along the ray from the receiver.
The gradient of the constant-offset travel-time field is a sum of the
two vectors
along the ray from the receiver.
The gradient of the constant-offset travel-time field is a sum of the
two vectors 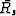 and
and 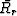 , and because the two vectors
have equal length
, and because the two vectors
have equal length 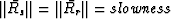 (from the
eikonal equation), the vector
(from the
eikonal equation), the vector 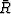 bisects the angle between
the vectors
bisects the angle between
the vectors 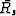 and
and 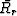 .
.
Figure 7:
The gradient of the constant-offset
travel-time field bisects the angle between the ray from the source
and the ray to the receiver.
|





Next: About this document ...
Up: Popovici : MZO
Previous: References
Stanford Exploration Project
12/18/1997
![]()
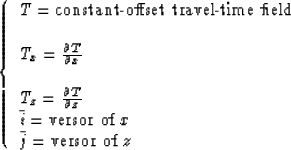
![]()
![]()
![]()