




Next: SUMMATION OVER THE DIFFRACTION
Up: Introduction
Previous: Introduction
The theory of the principal of diffraction summation can be derived using the
inhomogeneous acoustic wave equation (Schneider, 1978; Claerbout, 1986).
The simplified solution to the wave equation in an
arbitrary volume is given by the Kirchhoff integral.
A wavefield D can be expressed at any time and at any point as a
surface integral over the measured data D(x0,y0,z0,t).
Here x0,y0,z0 denote the coordinates of a coincident source-receiver
pair, and S is the surface on which the data were recorded.
Evaluating the extrapolated recorded wavefield for
all depths at time zero results in D(x,y,z,0), a three-dimensional
image of the subsurface:
| 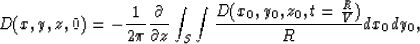 |
(1) |
where
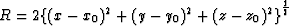 .This is the final formula used to migrate 3D zero-offset seismic
data. Therefore, in order to image the subsurface, the first step is to carry out the integration over the diffraction surface.
Let x,y,z be Cartesian coordinates with the origin at the surface of the
earth and the z-axis pointing vertically downwards.
A single scattering point (x1,y1,z1) in the subsurface has an
arrival time T for a coincident shot and receiver,
.This is the final formula used to migrate 3D zero-offset seismic
data. Therefore, in order to image the subsurface, the first step is to carry out the integration over the diffraction surface.
Let x,y,z be Cartesian coordinates with the origin at the surface of the
earth and the z-axis pointing vertically downwards.
A single scattering point (x1,y1,z1) in the subsurface has an
arrival time T for a coincident shot and receiver,
| 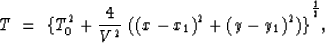 |
(2) |
where V is the velocity of propagation and T0=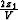 . Equation (1) represents the mapping
process of a point in the spatial domain (x,y,z) into a surface
in the space-time domain (x,y,t).
If V is a function of T0
only, the diffraction surface is a surface of revolution.
The time slice T=const cuts the diffraction surface in a circle
with center
at (x1,y1) and with
radius
. Equation (1) represents the mapping
process of a point in the spatial domain (x,y,z) into a surface
in the space-time domain (x,y,t).
If V is a function of T0
only, the diffraction surface is a surface of revolution.
The time slice T=const cuts the diffraction surface in a circle
with center
at (x1,y1) and with
radius 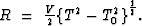 In mapping from one domain to the other,
scattering points are replaced by circles.
The convolution which replaces points by circles
can be expressed in the frequency domain by a multiplication
with a cosine filter.
In mapping from one domain to the other,
scattering points are replaced by circles.
The convolution which replaces points by circles
can be expressed in the frequency domain by a multiplication
with a cosine filter.





Next: SUMMATION OVER THE DIFFRACTION
Up: Introduction
Previous: Introduction
Stanford Exploration Project
12/18/1997