




Next: Initial and boundary conditions
Up: POINT SOURCE
Previous: POINT SOURCE
Let us assume the location of the point source is x0 on the surface.
With the coordinate transformation:
| 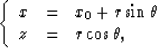 |
(3) |
we can derive the orthogonal equation in the polar coordinates:
| 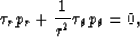 |
(4) |
where 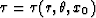 and
and 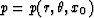 . The function p has a
physical meaning of surface horizontal slowness:
. The function p has a
physical meaning of surface horizontal slowness:
| 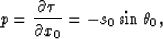 |
(5) |
where s0 is the slowness at the source location, 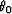 is the angle
between incident ray at the surface and the vertical.
Along each ray, the surface horizontal slowness p maintains to be constant.
Therefore, we can trace a ray by following the trajectory
of a contour line of p.
is the angle
between incident ray at the surface and the vertical.
Along each ray, the surface horizontal slowness p maintains to be constant.
Therefore, we can trace a ray by following the trajectory
of a contour line of p.





Next: Initial and boundary conditions
Up: POINT SOURCE
Previous: POINT SOURCE
Stanford Exploration Project
12/18/1997