Dip-picking and event-picking

Many algorithms in seismic data processing assume knowledge of the local dips of events on seismic sections. These local dips can be picked automatically by using the algorithm developed in the previous sections. Once the local dips are known on a uniform grid, we can trace the events on a seismic section. This process is called event-picking and has applications in structural interpretations and velocity analysis (Cunha Filho, 1991).

To pick an event, I first manually identify the event at one location, and then let the event-picking program trace the event to both sides using the equation:

$$t_{j\pm 1} = t_j \pm p_j \Delta x + {1 \over 2} {dp \over dx} (\Delta x)^2.$$ (13)

This analogous to the problem of finding the stream lines of a field when the gradients of the field are known. One may find a better method of solution, nevertheless, field data examples show that my method is adequate for these seismic applications.

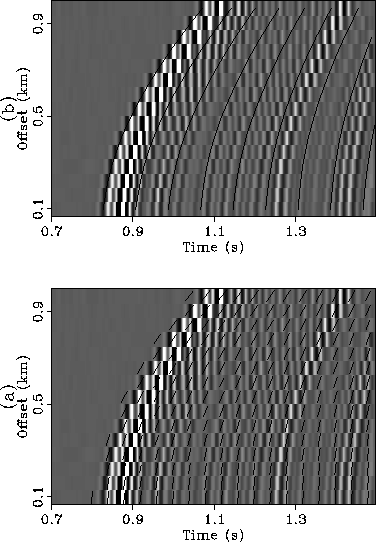
I applied my automatic picking algorithm to two field data gathers. The first one is a common midpoint (CMP) gather on which the events are seriously aliased at far offsets. The results of dip-picking are shown in Figure a. The picked local dips are displayed by the small line segments whose dips are equal to the dips of the events at those locations. We see that the small line segments are always parallel to the events shown on the background. The picked events are plotted on top of the raster image of the CMP gather, as shown in Figure b. The picked curves follow the correct trajectories of the events and ignore the coherent noises caused by aliasing.

To understand why this picking algorithm has an anti-aliasing property, let us look at an example of the objective function computed in the step of the constrained non-linear optimization. Figure shows the objective function E_n(t,x,p) for a fixed x. We see a sequence of minima that form a path from the left to the right. We also see some local minima that do not form complete paths. These local minima are created by the aliasing noise. If the unconstrained optimization is used, the algorithm might mistakenly pick some of the local minima. The constrained optimization forces the algorithm to pick a complete shortest-path that is displayed by the solid curve in Figure . For the same reason, the algorithm is not too insensitive to noise in data.

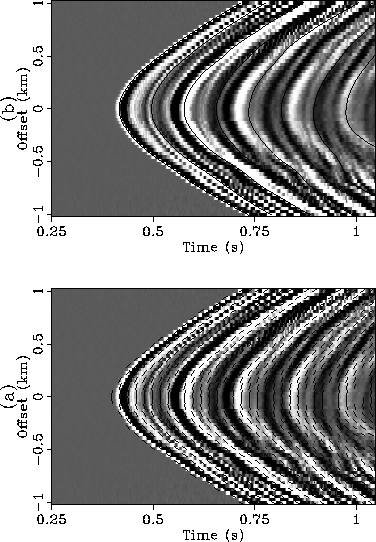
The second field data gather is a common-receiver gather recorded in a walk-away marine survey. This gather is collected with many shots on the surface and a receiver down in a well. The first arrival and several events that follow it are down-going waves. After 0.75 seconds, the up-going waves reflected from a deep layer start to interfere with the down-going waves. The picked local dips are represented by small line segments plotted in Figure a, and the picked events are displayed by the solid curves shown in Figure . Clearly, the algorithm performs reasonably well. It has no problem to pick the dip at locations where a single event is present. At locations where two or more events interfere with each other, the algorithm picks the dip of the event that is relatively stronger and whose dip value does not create an abrupt change of the dip function p(t). Looking carefully at the picked curve for the first arrival, we see that a ``pull-down'' of the first arrival at offset -0.6 km is correctly picked. This ``pull-down'' may be caused by a low velocity anomaly in the medium. This observation suggests a good accuracy of the algorithm. This event-picking method will probably be applied to traveltime inversion.

 

cmppick
Figure 1 Picking of a CMP gather: (a) dip-picking; (b) event-picking.

 

cmpobj
Figure 2 Objective function for a fixed x. The solid curve shows the shortest path. High intensities are large values.

 

vsppick
Figure 3 Picking of a common receiver gather: (a) dip-picking; (b) event-picking.