




Next: About this document ...
Up: Zhang: Residual depth migration
Previous: References
In Cartesian coordinates, the eikonal equation is
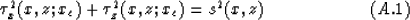
where xc=xs or xr are shot or receiver position.
Taking partial derivative of both sides of equation (A.1) with respect to xc
gives
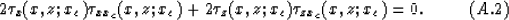
The right-hand side of the equation is zero because the slowness model is
independent of shot-receiver position.
Assume the derivatives of the traveltimes are continuous functions of (x,z)
and xc, we have
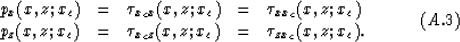
Combining equations (A.2) and (A.3) gives
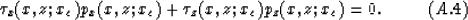
Using the relations between Cartesian coordinates and polar coordinates:

we can derive
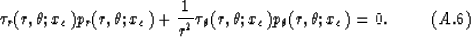





Next: About this document ...
Up: Zhang: Residual depth migration
Previous: References
Stanford Exploration Project
12/18/1997
![]()
![]()
![]()
![]()
![]()
![]()