




Next: Multichannel approach
Up: DESCRIPTION OF THE SUBTRACTION
Previous: DESCRIPTION OF THE SUBTRACTION
If we have an estimate S0 of the interfering signal the
following subtraction can be applied to the traces (Jenkins & Watts,1968):
| 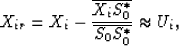 |
(2) |
where Xir is the residual, 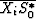 is the smoothed
cross-spectrum between the
i-th trace and the estimate, and
is the smoothed
cross-spectrum between the
i-th trace and the estimate, and 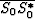 is
the smoothed power spectrum of the estimate.
is
the smoothed power spectrum of the estimate.
The problem with (2) is that often it is difficult
to obtain a good estimate S0. Now assume Si>>Ui and
substitute into (2) instead of S0 Xk-just one trace.
Remembering that Xk=Uk+Sk we get:
| 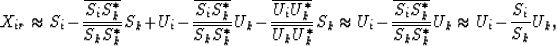 |
(3) |
and, rewriting the result:
| 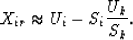 |
(4) |
Here Uk/Sk is a complex constant. The contribution of
the interfering source to each trace
has been reduced by the absolute value of this
constant (which is <<1 under our assumption), but the phase shift
between channels is preserved. To summarize, the magnitude of the
interfering source was reduced significantly without adding major
artifacts, and location of the weaker source is now more feasible.





Next: Multichannel approach
Up: DESCRIPTION OF THE SUBTRACTION
Previous: DESCRIPTION OF THE SUBTRACTION
Stanford Exploration Project
12/18/1997