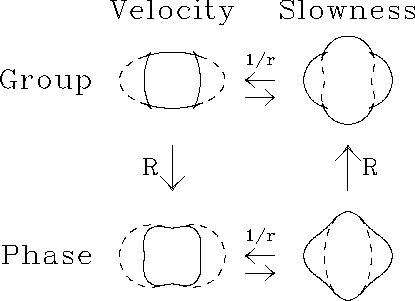 |
Figure 1 Group-four
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a transversely isotropic medium
and its vertical paraxial elliptic approximation represented
four different ways. Note that the dashed elliptical-approximation curve
plots as an ellipse in both the group-velocity and phase-slowness domains.
The vertical and horizontal velocities of the elliptical impulse response
define its principle axes; the corresponding vertical and horizontal
slownesses give the principle axes of the elliptical dispersion relation.
shows a transversely isotropic medium
and its vertical paraxial elliptic approximation represented
four different ways. Note that the dashed elliptical-approximation curve
plots as an ellipse in both the group-velocity and phase-slowness domains.
The vertical and horizontal velocities of the elliptical impulse response
define its principle axes; the corresponding vertical and horizontal
slownesses give the principle axes of the elliptical dispersion relation.
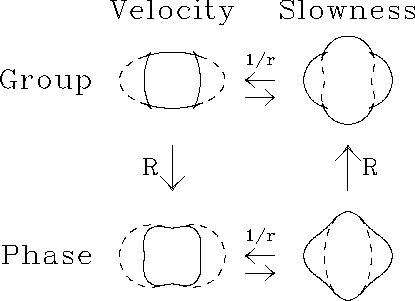 |
Group velocity (= impulse response), group slowness, phase velocity,
and phase slowness (= dispersion relation) plots for the qSV
mode of Greenhorn Shale (thick solid line) and an elliptically anisotropic
paraxial approximation to it (thin dashed line). The ``![]() ''
and ``
''
and ``![]() '' symbols indicate the recurring transformations
linking the four representations.
'' symbols indicate the recurring transformations
linking the four representations.
These vertical and horizontal velocities have simple geophysical interpretations. The vertical velocity of the paraxial elliptic approximation (equals the true vertical velocity) is what we need to do time-to-depth conversion. The horizontal velocity of the paraxial elliptic approximation (not the same thing as the true horizontal velocity) is what is required for NMO. (In a surface survey the sources and receivers are laid out along a horizontal line; if the vertical velocity were changed, it would effectively change the vertical scale of the survey, but the traveltime field recorded along the horizontal surface would remain unchanged. So it is horizontal velocity that matters. But it isn't the true horizontal velocity, because we're only considering NMO for near-vertical propagation. It is the horizontal velocity of the vertical paraxial elliptic approximation.)
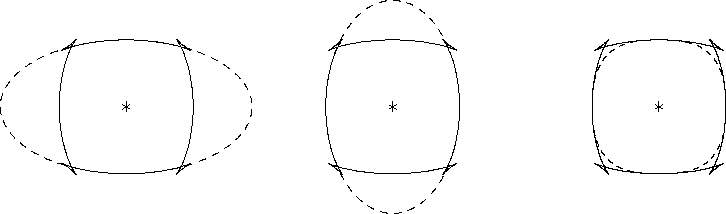 |
Three different approximations (dashed curves) to the qSV impulse-response surface of Greenhorn Shale (bold curves). On the left is the standard vertical paraxial elliptic approximation. In the center is the horizontal paraxial elliptic approximation. On the right is Muir's double-elliptic approximation.
 |
Three different approximations (dashed curves) to the qSV dispersion-relation surface of Greenhorn Shale (bold curves). On the left is the standard vertical paraxial elliptic approximation. In the center is the horizontal paraxial elliptic approximation. On the right is Muir's double-elliptic approximation; the fit is so close the dashed curve is hard to see.