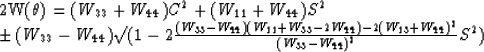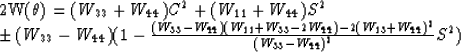Next: P plane waves about
Up: ELLIPTIC APPROXIMANTS FOR TI
Previous: SH plane waves about
Begin with the exact dispersion relations for P and SV waves.
| 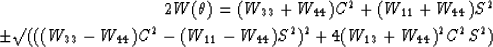 |
|
| (2) |
Now convert the cosines under the surd to sines.
Neglecting terms in S4.
Take constant out of bracket.
Expand the surd in powers of S2.
Return factor to original location
Simplify.
Reintroduce cosines.





Next: P plane waves about
Up: ELLIPTIC APPROXIMANTS FOR TI
Previous: SH plane waves about
Stanford Exploration Project
12/18/1997