![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) displays the
displays the ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) the
the
In this section we present the results of inverting the synthetic shot gathers
for specular reflectivity. A total of 141 shot gathers is migrated to
produce the estimates, which is identical to the field data requirement.
The migration model used is identical to the
elastic model of Table 1
for depths above the gas reflector, but continues
through the reservoir zone as a homogeneous halfspace with the properties
of the shale layer just above the gas sand.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) displays the
displays the ![]() elastic
elastic
![]() estimate, and Figure
estimate, and Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) the
the ![]() estimate,
for a single fixed surface position.
estimate,
for a single fixed surface position.
 |
 |
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) are true common depth point
images, as a function of source-receiver offset,
as opposed to migrated CMP gathers. Since each gather corresponds
to a constant x slice perpendicular to the (x,z) plane (the third
dimension being the offset coordinate), reflected events in the true CDP
are always flat (provided the velocity model is correct), independent
of reflector structure in the (x,z) plane. The near offset traces
in Figure
are true common depth point
images, as a function of source-receiver offset,
as opposed to migrated CMP gathers. Since each gather corresponds
to a constant x slice perpendicular to the (x,z) plane (the third
dimension being the offset coordinate), reflected events in the true CDP
are always flat (provided the velocity model is correct), independent
of reflector structure in the (x,z) plane. The near offset traces
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) have the correct relative
have the correct relative ![]() (peak) amplitudes to within
a few percent, as well as the correct Zoeppritz AVO response.
The shallow event at 1960 m is a little weak since it
is within a Fresnel zone of the mute pattern in the shot gathers. The
two reflections beneath the reservoir reflection at 2960 m are somewhat
attenuated due to the low Q values in the gas zone which are not
present in the migration model. Figure
(peak) amplitudes to within
a few percent, as well as the correct Zoeppritz AVO response.
The shallow event at 1960 m is a little weak since it
is within a Fresnel zone of the mute pattern in the shot gathers. The
two reflections beneath the reservoir reflection at 2960 m are somewhat
attenuated due to the low Q values in the gas zone which are not
present in the migration model. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is a contoured version of
an identical gather to Figure
is a contoured version of
an identical gather to Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , except it displays the calculated
, except it displays the calculated
![]() specular angles as a function of depth and source-receiver
offset. (This is actually the
specular angles as a function of depth and source-receiver
offset. (This is actually the ![]() estimate from the raw field
data, since the synthetic
estimate from the raw field
data, since the synthetic ![]() is more difficult to interpret
due to large zero-valued areas where no reflections exist). At the reservoir
depth, we see that the specular angles of reflection range from about
is more difficult to interpret
due to large zero-valued areas where no reflections exist). At the reservoir
depth, we see that the specular angles of reflection range from about
![]() to
to ![]() , which is correct to within
, which is correct to within ![]() compared to
raytraced values. The kinks in the contours at 1970 m and 2610 m are
accurate evidence of Snell's Law effects on
compared to
raytraced values. The kinks in the contours at 1970 m and 2610 m are
accurate evidence of Snell's Law effects on ![]() at abrupt changes
in the migration velocity model.
at abrupt changes
in the migration velocity model.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compares the migration estimate of
compares the migration estimate of ![]() at the
gas reflection (2960 m) to the
true Zoeppritz
at the
gas reflection (2960 m) to the
true Zoeppritz ![]() response as a function of specular angle.
The plotted open circles are the correct Zoeppritz values. The filled
circles are the migrated
response as a function of specular angle.
The plotted open circles are the correct Zoeppritz values. The filled
circles are the migrated ![]() estimates taken from combining
the information in Figures
estimates taken from combining
the information in Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
after applying a constant scale factor
normalization (loss of absolute amplitude in migration: only relative
amplitudes are recoverable).
,
after applying a constant scale factor
normalization (loss of absolute amplitude in migration: only relative
amplitudes are recoverable).
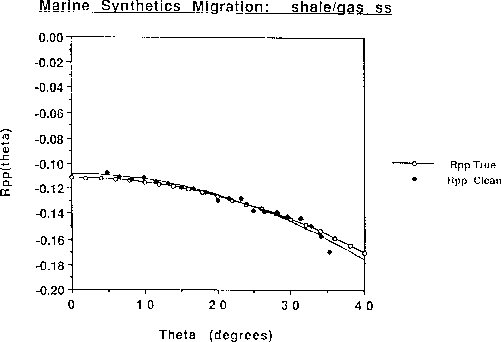 |
The extra curve is a quadratic fit
to the estimated ![]() . One can immediately see the good
agreement between the correct and estimated Zoeppritz specular reflectivity.
This level of accuracy in the migration estimate of Rpp on the gas event is
representative of the Rpp recovery on the other
reflection events in the gather.
In particular, it is evident that the finite aperture amplitude correction
inherent in our method has compensated well for the
marine end-on recording geometry in this variable background
model. It is important to note that the accurate estimation of Rpp,
. One can immediately see the good
agreement between the correct and estimated Zoeppritz specular reflectivity.
This level of accuracy in the migration estimate of Rpp on the gas event is
representative of the Rpp recovery on the other
reflection events in the gather.
In particular, it is evident that the finite aperture amplitude correction
inherent in our method has compensated well for the
marine end-on recording geometry in this variable background
model. It is important to note that the accurate estimation of Rpp,
![]() and the aperture correction are valid for (laterally)
heterogeneous media in general.
and the aperture correction are valid for (laterally)
heterogeneous media in general.
Finally, some preliminary stability issues in the ![]() estimation have been investigated. The migration has proved extremely
stable in the presence of random noise, certainly up to a s/n level
of 2:1. The migration amplitudes are less stable in the presence of
reasonable velocity-depth model errors (10%), but acceptable nonetheless.
As the velocity-depth errors increase, the kinematic error tends to
destroy the amplitude accuracy faster than the error due to geometric
divergence (as a function of offset in the Rpp gather). This
underlines the probable need for good residual migration velocity analysis
before inverting
estimation have been investigated. The migration has proved extremely
stable in the presence of random noise, certainly up to a s/n level
of 2:1. The migration amplitudes are less stable in the presence of
reasonable velocity-depth model errors (10%), but acceptable nonetheless.
As the velocity-depth errors increase, the kinematic error tends to
destroy the amplitude accuracy faster than the error due to geometric
divergence (as a function of offset in the Rpp gather). This
underlines the probable need for good residual migration velocity analysis
before inverting ![]() for elastic parameter variations.
for elastic parameter variations.
Considering amplitude loss effects, using an acoustic transmission loss
model instead of an elastic model produces no error on the normal incidence
Rpp values (no shear conversions at ![]() ), and
less than 10% decrease in amplitude at the far offsets at the target
zone. Considering anelastic Q attenuation
losses, prescaling the shot gathers with a time-variant
rms Q gain function before migration resulted in correct normal
incidence amplitudes, but an increase in far offset amplitudes in the
target zone of about 100%. Thus, it seems that pre-migration
Q amplitude compensation may not be appropriate for preserving
migrated
), and
less than 10% decrease in amplitude at the far offsets at the target
zone. Considering anelastic Q attenuation
losses, prescaling the shot gathers with a time-variant
rms Q gain function before migration resulted in correct normal
incidence amplitudes, but an increase in far offset amplitudes in the
target zone of about 100%. Thus, it seems that pre-migration
Q amplitude compensation may not be appropriate for preserving
migrated ![]() amplitudes, but rather, the compensation needs
to be done properly in the depth model domain during depth migration.
Finally, approximations to the WKBJ geometrical divergence amplitude
within the migration by simple factors such as 1/r or
amplitudes, but rather, the compensation needs
to be done properly in the depth model domain during depth migration.
Finally, approximations to the WKBJ geometrical divergence amplitude
within the migration by simple factors such as 1/r or ![]() produced accurate amplitudes at normal incidence,
and were about 10% too weak at far offsets along the gas reflection.
Although this error will increase for targets shallower than 3000 m, the
approximation seems acceptable for this earth model and acquisition
geometry. However, performing a time-variant divergence correction as a
function of the rms velocity (
produced accurate amplitudes at normal incidence,
and were about 10% too weak at far offsets along the gas reflection.
Although this error will increase for targets shallower than 3000 m, the
approximation seems acceptable for this earth model and acquisition
geometry. However, performing a time-variant divergence correction as a
function of the rms velocity (![]() ) greatly overemphasized
the far offset amplitudes. Hence, as with Q compensation, it seems most
reasonable to make approximate compensation for geometric divergence in the
spatial domain (depth migration), and not in the time
domain (time migration).
) greatly overemphasized
the far offset amplitudes. Hence, as with Q compensation, it seems most
reasonable to make approximate compensation for geometric divergence in the
spatial domain (depth migration), and not in the time
domain (time migration).