




Next: CONCLUSIONS
Up: Cunha: Walsh function decomposition
Previous: WALSH FUNCTIONS
I use the same simple synthetic model as in Cunha (1990) to compare
the results obtained with different inversion schemes.
The model consists of an isotropic layer in an isotropic
background (Vz=Vx in both the layer and the background).
The layer is not centered, and its size is not a multiple of
the layer size used in the inversion schemes.
isoinv
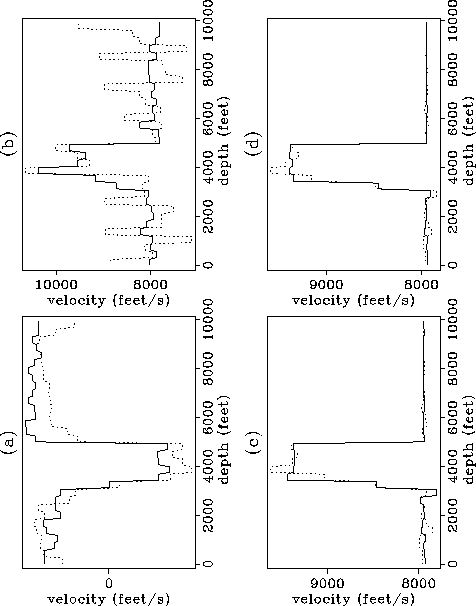
Figure 3 Inversion results for the one-layer isotropic model, using
different algorithms: (a) square function decomposition (nonlinear),
(b) Walsh function decomposition (nonlinear),
(c) linearized inversion with layer-parametrization, and (d)
the same as in c, but with the derivative term introduced
into the objective function.continuous line represents Vx and
dotted line represents Vz.

Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a and
a and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b show that,
contrary to what we would expect, the results obtained with the Walsh
functions are inferior to the ones obtained with the sine- and
cosine-like square functions. Although Walsh functions form
a complete set, their orthogonality impedes
further steps from correcting errors in previously estimated
components of the model in this kind of iterative scheme. Moreover,
both nonlinear schemes are inferior to the linearized
algorithms shown in Figures
b show that,
contrary to what we would expect, the results obtained with the Walsh
functions are inferior to the ones obtained with the sine- and
cosine-like square functions. Although Walsh functions form
a complete set, their orthogonality impedes
further steps from correcting errors in previously estimated
components of the model in this kind of iterative scheme. Moreover,
both nonlinear schemes are inferior to the linearized
algorithms shown in Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c and
c and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) d.
The result in
d.
The result in ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c was obtained with an iterative scheme that uses
the least-squares solution of equation (8) by
successively increasing (by a power of 2) the number of layers at each step.
The difference between
c was obtained with an iterative scheme that uses
the least-squares solution of equation (8) by
successively increasing (by a power of 2) the number of layers at each step.
The difference between ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c and
c and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) d is the introduction
into the objective function of an extra term that corresponds to
the difference between the traveltime-derivatives relative to
the receiver positions. As a result the solution
for Vz in
d is the introduction
into the objective function of an extra term that corresponds to
the difference between the traveltime-derivatives relative to
the receiver positions. As a result the solution
for Vz in ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) d becomes more stable since with this term
the inversion will try to fit not only the traveltimes, but also
the form of the traveltime curves.
d becomes more stable since with this term
the inversion will try to fit not only the traveltimes, but also
the form of the traveltime curves.





Next: CONCLUSIONS
Up: Cunha: Walsh function decomposition
Previous: WALSH FUNCTIONS
Stanford Exploration Project
12/18/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif)