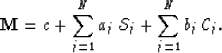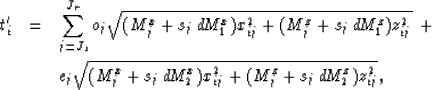Next: Linearized Inversion
Up: INVERSION SCHEMES
Previous: INVERSION SCHEMES
In a previous report (Cunha, 1990) I used a set of sine- and cosine-
like square functions to describe the model:
| 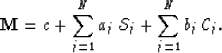 |
(3) |
This choice of model decomposition led to an iterative perturbation
scheme that estimates different components of the model at each iteration,
starting with the homogeneous solution and successively increasing the
frequency of the perturbation.
The predicted traveltimes are given by
| 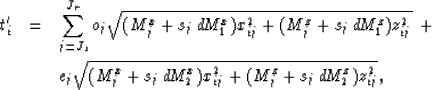 |
|
| (4) |
where oj, ej, and sj are defined as follows:
| 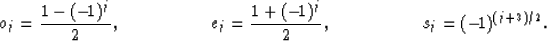 |
(5) |
In the above equations j is the layer index, Js and Jr are the
indices of the
source and receiver layers, xij and zij are the horizontal
and vertical distances traveled inside the layer j by the ray
associated with source-receiver i.
Using equation (4) in the objective function (2),
the inversion problem can be easily solved with a nonlinear optimization
algorithm (like the Downhill Simplex method) since only four parameters
are inverted at each step: 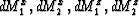 .
.





Next: Linearized Inversion
Up: INVERSION SCHEMES
Previous: INVERSION SCHEMES
Stanford Exploration Project
12/18/1997