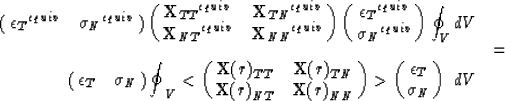THE EQUIVALENT HOMOGENEOUS MEDIUM

We can define then an average medium, which has the same integral properties as the original heterogeneous medium:

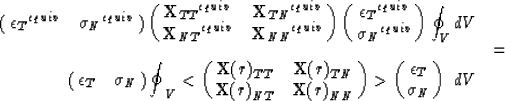$$\begin{eqnarray} \pmatrix{{ {\epsilon}_{T} }^{equiv} & { {\sigma}_{N} }^{equiv} ... ..._{NN} \cr} \gt \pmatrix{ {\epsilon}_{T} \cr {\sigma}_{N} \cr}~dV&\end{eqnarray}$$ (16)

For the homogeneous equivalent we know that it is energetically equivalent but in the interior stress distribution different from the heterogeneous medium. They share the same integral properties, and the stress and strain will be on the average equivalent. Taking the heterogeneous medium and applying a static force to its exterior boundaries results in a static stress and strain distribution within the body. This means stress and strain are functions of the spatial coordinates only. The stress and strain values are uniquely determined by the stiffness and by the external forces applied to the exterior surface. If we apply the same external forces to the homogeneous medium we will in general not end up with the same displacements as observed in the heterogeneous case, but on the average over a region much larger than the scale of the heterogeneity we will have the same result.